今回の記事では「等比数列」についてイチから解説してきます。
等比数列というのは…
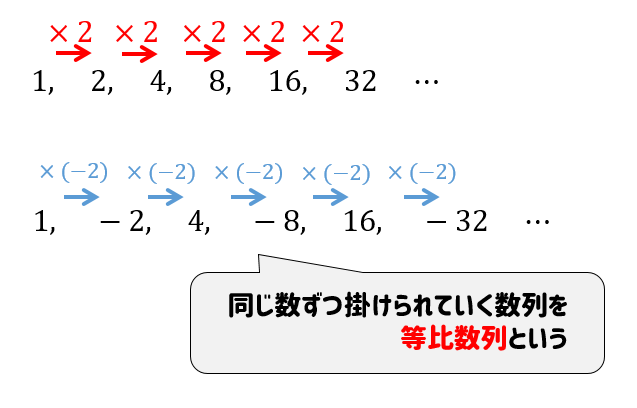
このように、同じ数だけ掛けられていく数列のことだね。
この数列の第\(n\)番目の数は?
数列の和はどうなる?
といった基本的な問題の解き方などを学んでいこう!
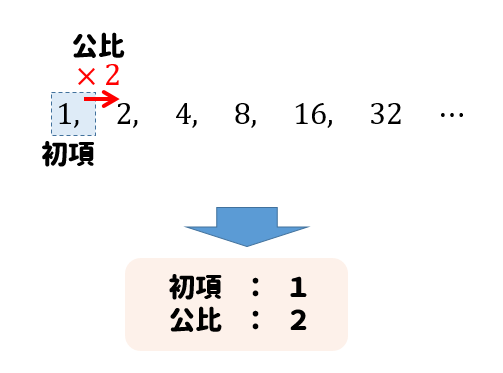
ちなみに、一番最初の項を初項、等比数列の変化していく値のことを公比というので、それぞれ覚えておいてね。
それぞれの項目のところに解説動画も用意しているので参考にしてくださいね^^
等比数列の考え方!【一般項の公式】
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
等比数列の一般項を求める公式
$$a_n=ar^{n-1}$$
$$a:初項 r:公比$$
この公式を覚えてしまえば、等比数列の一般項は楽勝です(^^)
なぜ、このような公式になるのか。
これはとてもシンプルなことなので、サクッと理解しちゃいましょう。
等比数列の項を求める場合
その項は、初項からどれだけ公比が掛けられて出来上がったものなのか?
を考えてみましょう!
例えば、次の等比数列を考えてみると
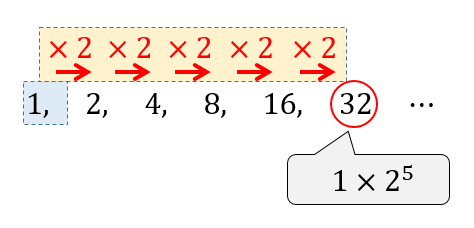
第6項の数は、初項から公比が5回掛けられて出来上がっているってことが分かるよね!
第10項であれば、初項から公比を9回。
第100項であれば、初項から公比を99回。
というように、求めたい項からマイナス1した回数だけ公比が掛けられていることに気が付くはずです。
そうなれば、第\(n\)項の場合には?
文字がでてきても考えは同じだね!マイナス1をした\((n-1)\)回だけ公比が掛けられているってことだ。
つまり!
等比数列の第\(n\)項は、初項に公比を\((n-1)\)回だけ掛けた数ってことなので
$$\begin{eqnarray}a_n=ar^{n-1} \end{eqnarray}$$
こういった公式ができあがるわけですね!
等比数列の一般項に関する問題解説!
では、一般項の公式を使って問題を解いてみましょう。
初項が\(3\)、公比が\(-2\)である等比数列\(\{a_n\}\)の一般項を求めなさい。
また、第\(4\)項を求めなさい。
第\(3\)項が\(18\)、第\(6\)項が\(486\)である等差数列\(\{a_n\}\)の一般項を求めなさい。
また、\(162\)は第何項になるか求めなさい。
3つの等比数列【等比中項】
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
等比中項
3つの項の等比数列\(a, b, c\)について、次の式が成り立つ。
$$b^2=ac$$
こうやって公式だけ見てしまうと難しく感じてしまいますが、単純なことです。
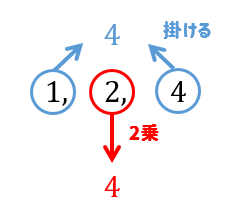
真ん中の数を2乗すると、両端の数を掛けたものに等しくなるってことですね!
このとき、真ん中にある項のことを両端の項の等比中項といいます。
よくでてくる用語なので覚えておきましょう!
なぜ、等比数列はこのような関係になっているのか。
これは簡単に証明ができます。
\(a\)と\(b\)、\(b\)と\(c\)の比を考えてみましょう。
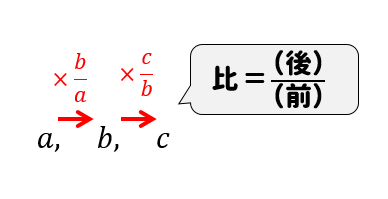
等比数列とは、その名の通り
比が等しいわけですから
$$\frac{b}{a}=\frac{c}{b}$$
という関係式ができます。
これを変形すると
$$\begin{eqnarray}\frac{b}{a}&=&\frac{c}{b}\\[5pt]\frac{b}{a}\times ab &=&\frac{c}{b} \times ab\\[5pt]b^2&=&ac \end{eqnarray}$$
となるわけですね!
簡単、簡単(^^)
等比中項に関する問題解説!
では、等比中項を使って問題を解いてみましょう。
数列 \(9, x, 4\) が等比数列であるとき、\(x\)の値を求めなさい。
数列\(4, a, b\) および数列\(b, 40, 64\) は等比数列である。このとき、\(a, b\) の値をそれぞれ求めなさい。
等比数列の和【和の公式】
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
等比数列の和を求める公式
\(r\neq 1\) のとき
$$S_n=\frac{a(1-r^n)}{1-r}=\frac{a(r^n-1)}{r-1}$$
\(r=1\) のとき
$$S_n=na$$
$$a:初項 r:公比 n;項数$$
どのようにして、等比数列の公式を導くのか。
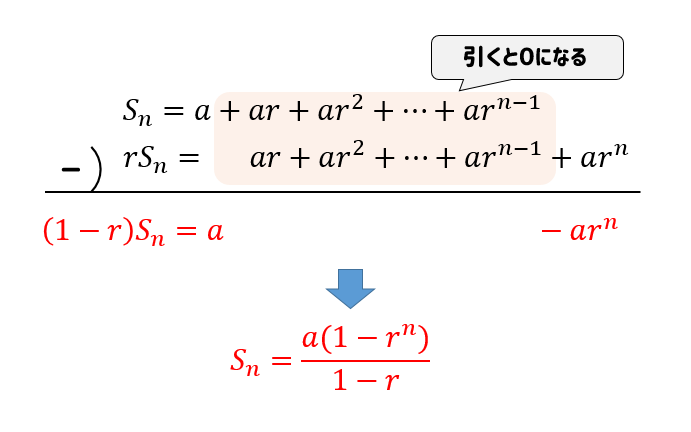
このように等比数列の和に公比を掛けた式をつくり、それぞれを引くことによって導くことができます。
また、等比数列の和の公式には
$$S_n=\frac{a(1-r^n)}{1-r}=\frac{a(r^n-1)}{r-1}$$
このように2パターンあります。
これは、公比の値からどちらの式を使うのが適切かを判断して使用していきます。
\(r>1\) のときには、\(S_n=\frac{a(r^n-1)}{r-1}\) の式を。
\(r<1\) のときには、\(S_n=\frac{a(1-r^n)}{1-r}\) の式を使うと計算が少しラクになります。
等比数列の和に関する問題解説!
初項\(1\)、公比\(2\)の等比数列の初項から第\(n\)項までの和を求めなさい。
初項\(3\)、公比\(-2\)の等比数列の初項から第\(5\)項までの和を求めなさい。
第\(2\)項が\(3\)、初項から第\(3\)項までの和が\(13\)である等比数列の初項と公比を求めなさい。
等比数列の公式【まとめ!】
では、最後に等比数列の公式をまとめておきましょう!
等比数列の一般項を求める公式
$$a_n=ar^{n-1}$$
$$a:初項 r:公比$$
等比中項
3つの項の等比数列\(a, b, c\)について、次の式が成り立つ。
$$b^2=ac$$
等比数列の和を求める公式
\(r\neq 1\) のとき
$$S_n=\frac{a(1-r^n)}{1-r}=\frac{a(r^n-1)}{r-1}$$
\(r=1\) のとき
$$S_n=na$$
$$a:初項 r:公比 n;項数$$












コメントを残す