【高校数学】集合の記号の意味、使い方まとめ！

高校数学で学習する集合の記号について

絶対に覚えておきたいものをまとめておきます。

\(x \in A\)	\(x\)は\(A\)に属する
\(x \notin A\)	\(x\)は\(A\)に属さない
\(A \subset B\)	\(A\)は\(B\)に含まれる（部分集合）
\(A=B\)	\(A\)と\(B\)は等しい
\(\emptyset \)	空集合（要素が1つもない集合）
\(A \cap B\)	\(A\)と\(B\)の共通部分、\(A,B\)どちらにも含まれる要素全体の集合
\(A \cup B\)	\(A\)と\(B\)の和集合、\(A,B\)の少なくとも一方に含まれる要素全体の集合
全体集合\(U\)	1つの集合\(U\)を定めて、その集合の要素や部分集合について扱うとき、集合\(U\)を全体集合という
\(\overline{ A }\)	\(A\)の補集合、全体集合の要素で\(A\)に属さない要素全体の集合

 

それぞれの意味や使い方、問題演習については本文にて解説しています。

 

要素、属するとは

範囲がはっきりしたものの集まりのことを集合といいます。

（例：1から10までの整数の集まり）

その集合のなかに入っている1つ1つのもののことを要素といいます。

 

みんなが知っているようなアイドルグループで具体例を挙げてみると分かりやすいかな

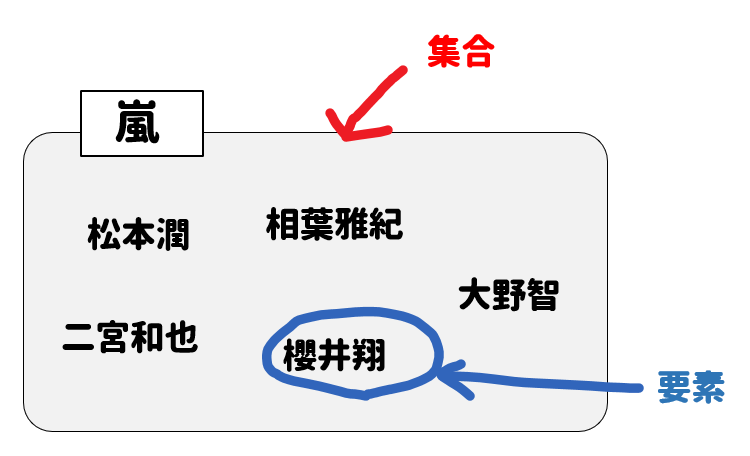
ここでいうと、嵐というグループが集合、メンバー1人1人が要素ってことになるね。

集合＝グループ

要素＝メンバー

って、考えておくとイメージしやすいかもね！

数学の世界だと、集合にはAとかBって名前がついていて、要素には1，2，3…といった数字が入るようになるよ。

 

 

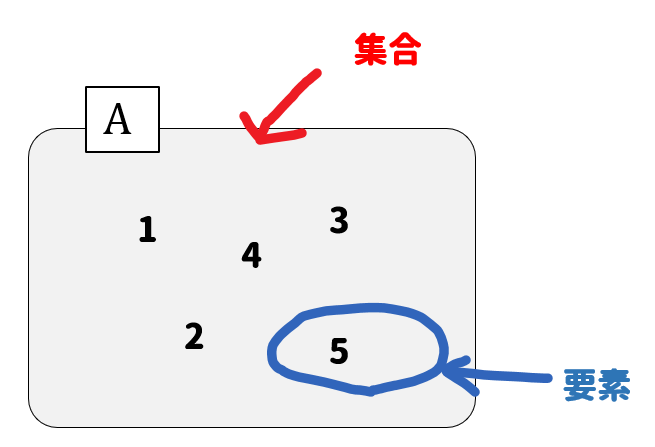
そして、要素が集合の中に入っているときには属するといいます。

松本潤は嵐に属する。

といった感じだね。

これを数学の記号\(\in\)を使って

\(松本潤 \in 嵐\)と表します。

 

数学の話に戻すと…

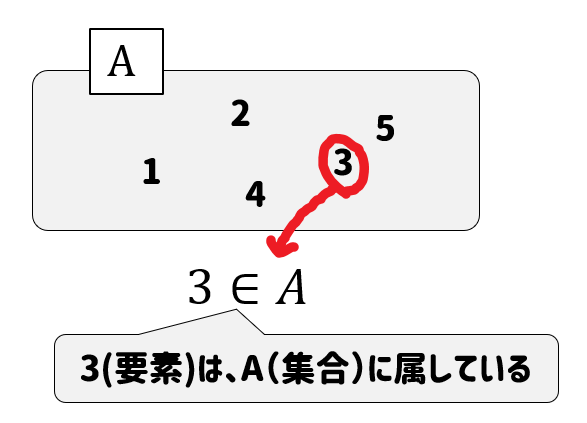
こんな感じだね。

 

ちなみに、属さないというのは、\(\notin\)を使って次のように表します。

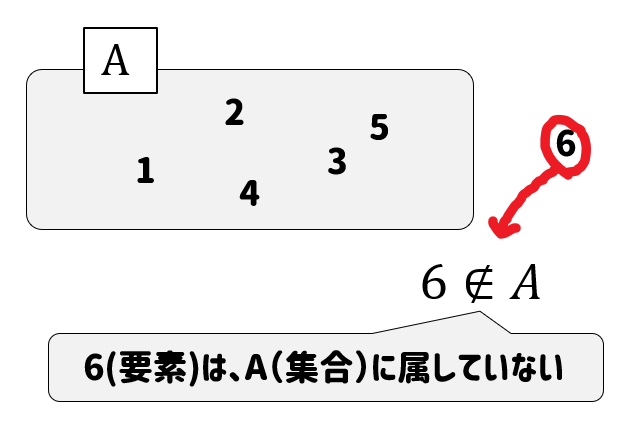
部分集合とは

2つの集合A、Bについて、Aのすべての要素がBの要素でもあるとき、AはBの部分集合といいます。

文章で説明すると難しく見えちゃうな(^^;)

図を見てみると分かりやすいです。

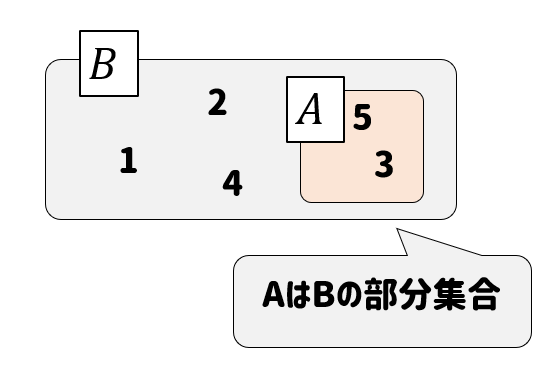
このように一方の集合が、もう一方の集合の中にすっぽりと入っている状態のことを部分集合といいます。

記号を使って表すと

$$\large{A \subset B}$$

$$\large{B \supset A}$$

となります。

不等号と同じで、大きい集合の方に口が開いている感じだね。

 

ここでちょっと疑問に思った人はいないかな？

\(x\in A\)、\(A \subset B\)

この2つって何が違うの？両方とも含まれてるようなイメージだよね？

って考えた人もいるのではないでしょうか？

これは、よく質問いただく内容です。

 

違いのポイントは簡単。

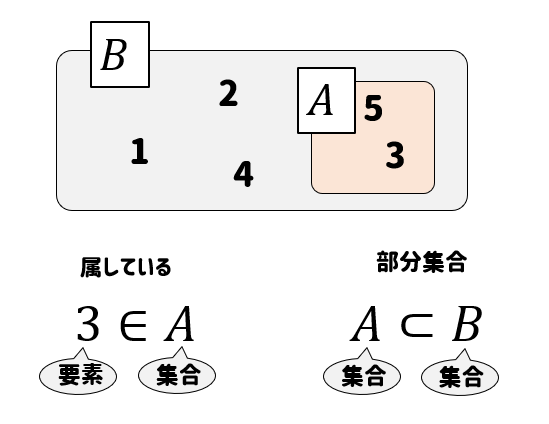
要素と集合の比較であれば、\(\in\)。

集合と集合の比較であれば、\(\subset\)を使います。

 

ちなみに、2つの集合の要素がすべて同じであるときには

$$\large{A = B}$$

このようにイコールを使って表します。

 

空集合とは

要素がない集合のことを空集合といい、Φ（ファイ）で表します。

 

全然難しくありません。

からっぽな集合が空集合ってことです。

からっぽが故に、どんな集合にも潜り込むことができます。

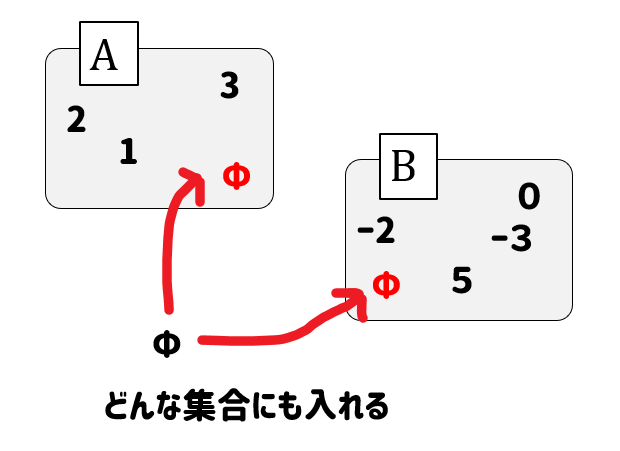
つまり、空集合とはすべての集合に対して部分集合になれるということです。

共通部分、和集合とは

 

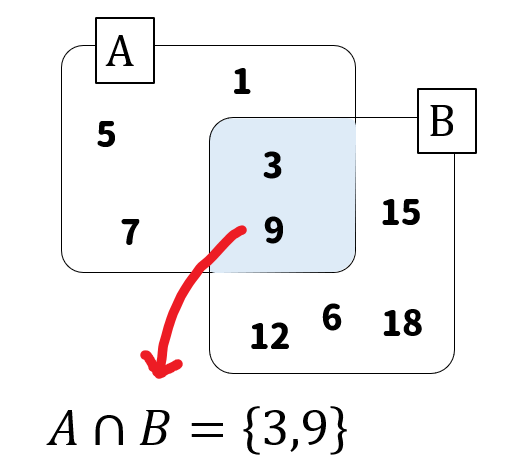
集合A、Bのどちらにも属する要素全体の集合をAとBの共通部分といい、\(\cap\)という記号を使って表します。

簡単に言うと、2つの集合が重なっている部分です。

 

集合A、Bのどちらか一方に属する要素全体の集合をAとBの和集合といい、\(\cup\)という記号を使って表します。

簡単に言うと、2つの集合をあわせたものです。

 

AとBに共通している要素は

\(A=\{1,\color{red}{2},3,\color{red}{4},5\}\)、\(B=\{\color{red}{2,4},6,8\}\)なので

$$A\cap B=\{2,4\}\cdots(解)$$

 

和集合は、AとBの要素をすべて合わせたものだから

$$A\cup B=\{1,2,3,4,5,6,8\}\cdots(解)$$

補集合とは

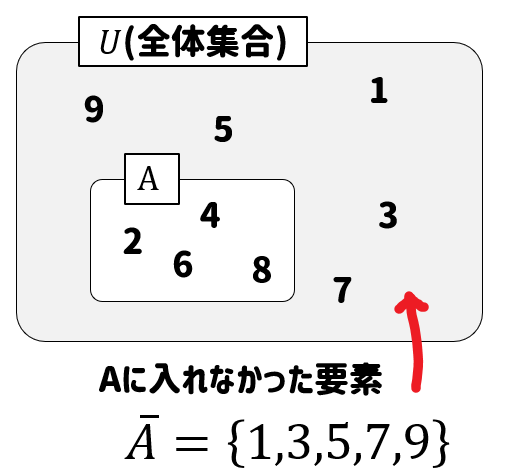
全体集合\(U\)の部分集合\(A\)に対して、\(A\)に属さない\(U\)の要素全体の集合を\(A\)の補集合といいます。

\(\overline{ A }\)という記号を使って表します。

これまた説明が難しいですが…

簡単にいうと、\(A\)に入れなかった要素の集まり。

これが補集合です。

 

ちなみに、補集合には次のような性質があります。

あわせて覚えておきましょう。

まとめ！

集合の記号って、いかにも数学って感じで難しく見えちゃいます。

だけど、同じ部分は？合わせると？じゃないやつは？など

実際には単純なことして言ってませんよね。

 

覚えるまでにはちょっと時間がかかるかもしれませんが、簡単なことなのでなるべく早めにサクッと理解しておきましょう。