こんにちは!数スタの小田です。
今回は高校数学Ⅰで学習する三角比の単元から「取りうる値の範囲」についてイチから解説します。
取り上げる問題はこちら!
【問題】次の式のとりうる値の範囲を求めなさい。
(1) \(2\sin{\theta}-1\) \((0°≦\theta≦180°)\)
(2) \(-3\cos{\theta}+1\) \((0°≦\theta≦180°)\)
(3) \(\sqrt{2}\sin{\theta}+3\) \((60°≦\theta≦135°)\)
(4) \(\sqrt{3}\tan{\theta}-3\) \((30°≦\theta<60°)\)
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(1)の解説 \(\sin{\theta}\)の範囲
【問題】次の式のとりうる値の範囲を求めなさい。
(1) \(2\sin{\theta}-1\) \((0°≦\theta≦180°)\)
\(\sin{\theta}\)の範囲は単位円の\(y\)座標の範囲を見ていきます!
まずは円を書いて0°から180°までの範囲に色を付けます。
そして、色がついている部分の\(y\)座標の範囲をチェックして\(\sin{\theta}\)の範囲を求めましょう。

すると、このようにして式の範囲を求めることができます!
\(\sin{\theta}\)の範囲を求めたら、そこから少しずつ式を変形してもとに式に近づけていきましょう。
(2)の解説 \(\cos{\theta}\)の範囲
【問題】次の式のとりうる値の範囲を求めなさい。
(2) \(-3\cos{\theta}+1\) \((0°≦\theta≦180°)\)
\(\cos{\theta}\)の範囲は単位円の\(x\)座標の範囲を見ていきます!
まずは円を書いて0°から180°までの範囲に色を付けます。
そして、色がついている部分の\(x\)座標の範囲をチェックして\(\cos{\theta}\)の範囲を求めましょう。
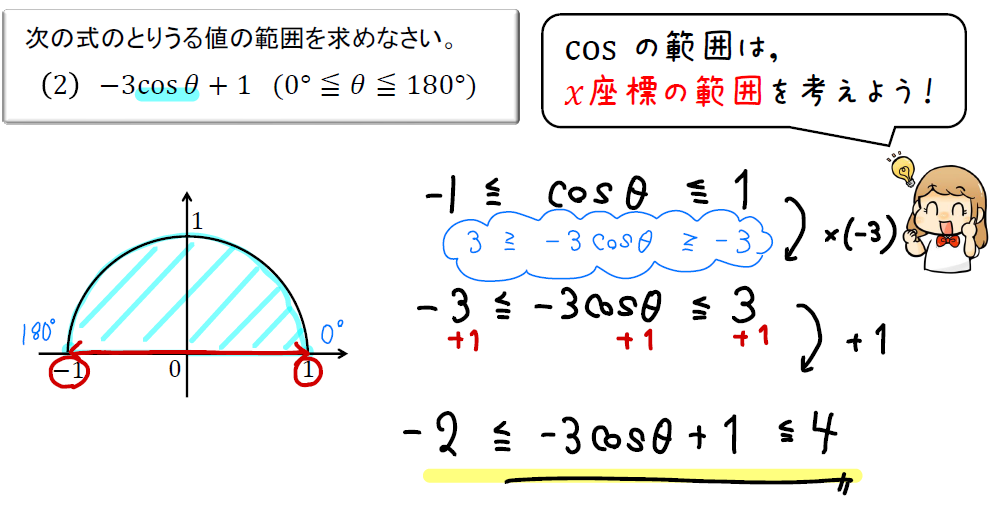
すると、このように式の範囲が求まりますね!
式を変形するとき、負の数をかけると不等号の向きが逆になってしまいますので、そこでミスがないように注意してください。
(3)の解説 \(\sin{\theta}\) 60°~135°
【問題】次の式のとりうる値の範囲を求めなさい。
(3) \(\sqrt{2}\sin{\theta}+3\) \((60°≦\theta≦135°)\)
\(\sin{\theta}\)の範囲は単位円の\(y\)座標の範囲を見ていきます!
まずは円を書いて60°から135°までの範囲に色を付けます。
そして、色がついている部分の\(y\)座標の範囲をチェックして\(\sin{\theta}\)の範囲を求めましょう。

色がついた部分の\(y\)座標を見ると、90°のときに最大、135°のときに最小になることがわかりますね。
そこから \(\sin{\theta}\) の範囲を上の画像のように求めてください。
図がないと \(y\)の範囲がイメージしにくいので、必ず図を書くようにしてくださいね!
(4)の解説 \(\tan{\theta}\) の範囲
【問題】次の式のとりうる値の範囲を求めなさい。
(4) \(\sqrt{3}\tan{\theta}-3\) \((30°≦\theta<60°)\)
\(\tan{\theta}\)の範囲は傾きの範囲を見ていきます!
まずは円を書いて30°から60°までの範囲に色を付けます。
そして、色がついている部分の傾きの範囲をチェックして\(\tan{\theta}\)の範囲を求めましょう。
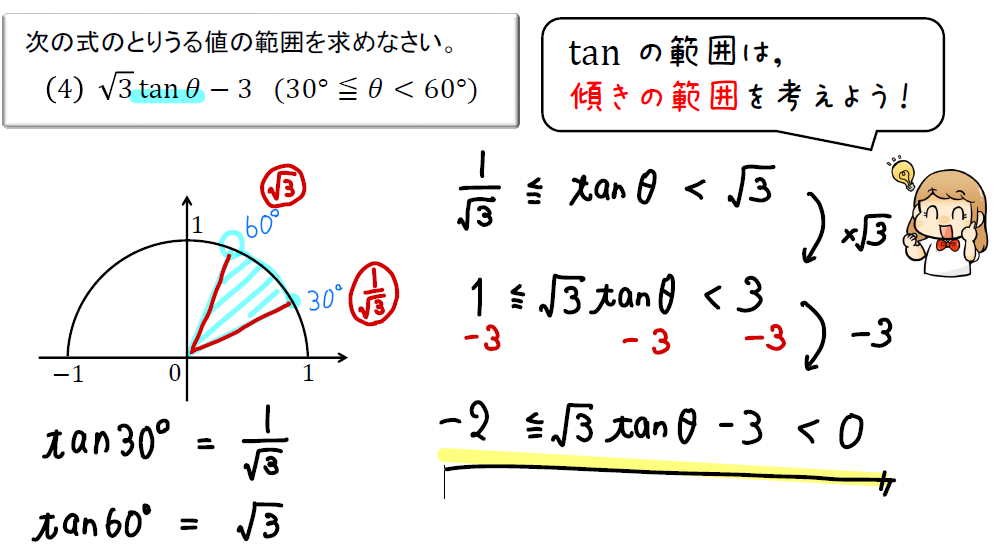
直線の傾きをチェックすると、30°のときが最小、60°のときが最大になることがわかりますね。
それぞれの角度での \(\tan\) の値をチェックすれば、上の画像のように範囲が求まります。
60°のときは「<(含まない)」となっているので、範囲を表す不等式でも「<」を使うようにしてくださいね!
まとめ
というわけで、今回は三角比のとりうる値の範囲について解説しました。
全部理解できたかな??
\(\cos{\theta}\) → \(x\)座標
\(\sin{\theta}\) → \(y\)座標
\(\tan{\theta}\) → 傾き
このポイントをおさえた上で、単位円を書きながらチェックしていけば簡単に求めることができますね^^
数学Ⅱで学習する三角関数の単元でも活用していく知識になるので、今のうちにしっかりと理解しておいてください!
では、今回は以上!
















コメントを残す