【三角比の面積】公式と計算方法は？いろんな場面での使い方を解説！

今回は高校数学Ⅰで学習する三角比の単元から

三角形の面積を求める公式

について解説していきます。

公式はシンプルなものですが、問題ではいろんなバリエーションが存在します。

しっかりと理解を深めて、三角比の得点をアップさせちゃいましょう！

今回の内容はこちらの動画でも解説しています！

【三角比の面積】公式と証明

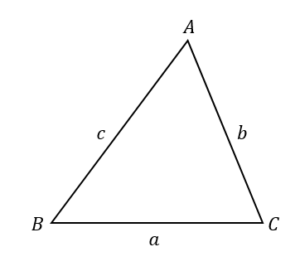
三角比の面積公式

$$\begin{eqnarray}S&=&\frac{1}{2}bc\sin A\\[5pt]&=&\frac{1}{2}ca\sin B\\[5pt]&=&\frac{1}{2}ab\sin C \end{eqnarray}$$

このような公式を使って三角形の面積を求めることができます。

なぜ？

疑問が湧いてきますね。

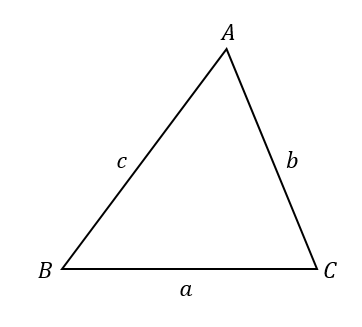
説明は簡単なことです。三角形の面積って

この計算式で求めることができるよね。

辺BCを底辺と考えた場合

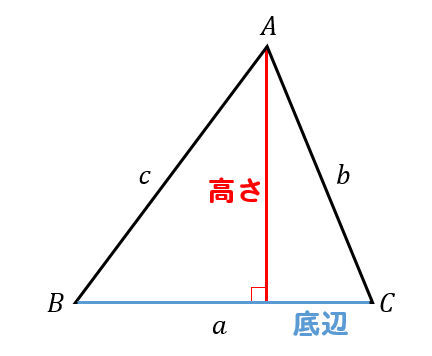
赤線の部分を高さとして考えることができます。

そして、この赤線部分は

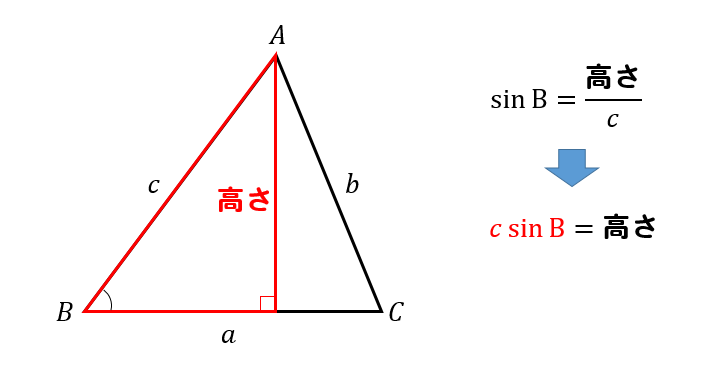
このように直角三角形を考えることで、\(c\sin B\) と表すことができます。

よって、三角形の面積は

$$\begin{eqnarray}三角形の面積&=&底辺\times 高さ\times\frac{1}{2}\\[5pt]&=&a\times c\sin B\times\frac{1}{2}\\[5pt] &=&\frac{1}{2}ac\sin B\end{eqnarray}$$

これは鈍角三角形であっても同じように考えることができます。

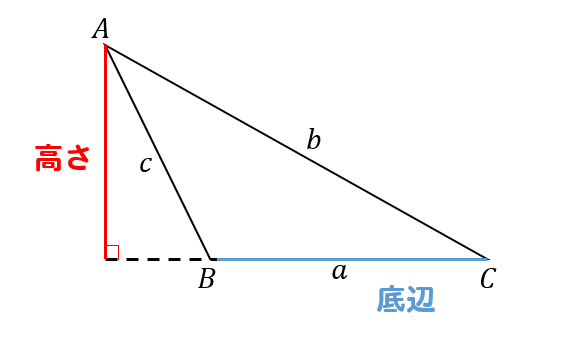
三角形の高さは、直角三角形を作り、\(\sin\)を使うことで表すことができます。

つまり、三角形の面積公式は三角比を使って高さを表してるから、あのような式になるということですね。

では、次の章では公式を使って計算をするやり方についてみていきましょう。

【三角比の面積】問題と計算のやり方

まずは、簡単なイメージ図を書いてみると分かりやすいです。

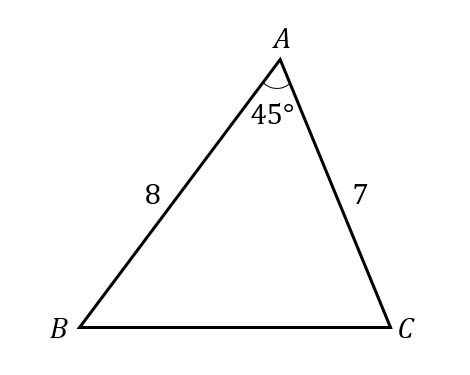
三角形の面積公式は、2辺と間にある角を使うので

$$\begin{eqnarray}S&=&\frac{1}{2}bc\sin A\\[5pt]&=&\frac{1}{2}\cdot 7\cdot 8\sin 45°\\[5pt]&=&28\cdot \frac{1}{\sqrt{2}}\\[5pt]&=&14\sqrt{2} \end{eqnarray}$$

とっても簡単ですね(^^)

次のような鈍角三角形でも同様です。

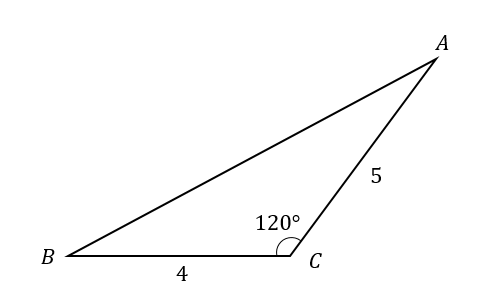
$$\begin{eqnarray}S&=&\frac{1}{2}ab\sin C\\[5pt]&=&\frac{1}{2}\cdot 4\cdot 5\sin 120°\\[5pt]&=&10\cdot \frac{\sqrt{3}}{2}\\[5pt]&=&5\sqrt{3} \end{eqnarray}$$

では、ちょっとひねりを加えて次の問題。

【三角比の面積問題】

次のような△ABCの面積を求めなさい。

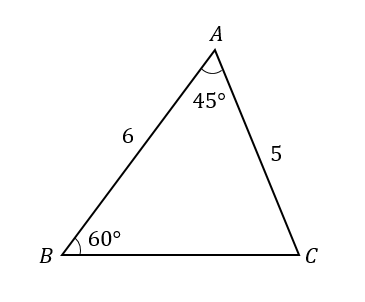
あれ…？

角度が2つある。どっちを使えばいいんだっけ…

と、悩んではいけませんよ！

三角形の面積公式を使うためには、2辺と間の角が必要になります。

なので、角Aの部分を使って計算を進めていきます。

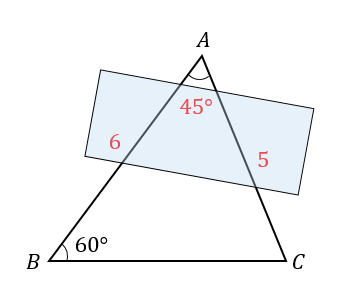
$$\begin{eqnarray}S&=&\frac{1}{2}bc\sin A\\[5pt]&=&\frac{1}{2}\cdot 6\cdot 5\sin 45°\\[5pt]&=&15\cdot \frac{1}{\sqrt{2}}\\[5pt]&=&\frac{15\sqrt{2}}{2} \end{eqnarray}$$

角Bを使って面積を求めたければ

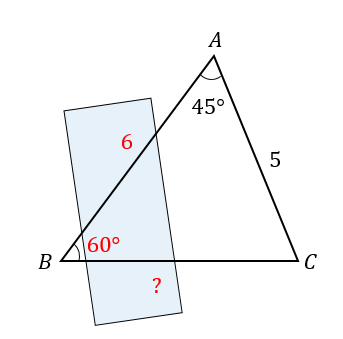
辺\(a\)の長さが必要になりますね。

このように与えられた情報から、どの部分を使えばよいのかを自分で判断する必要があります。

だけど、これは難しいことではありませんね。

面積を求めるためには、2辺と間の角が必要！

これを頭に入れておきましょう(^^)

【三角比の面積】3辺から面積を求める計算

ん？

どこにも角度が書いてないじゃないか！！

ということで、面積公式を使うことができません…

こういう場合には、面積公式に必要な\(\sin\)の値を求めることからスタートします。

とは言っても、いきなり\(\sin\) の値を求めることは難しいので一旦、\(\cos\) の値を求める。

その後、\(\sin\) に変換するといった流れでやっていきます。

角Aに注目して、余弦定理を使うと

$$\begin{eqnarray}\cos A&=&\frac{9^2+8^2-5^2}{2\cdot 9\cdot 8}\\[5pt]&=&\frac{120}{2\cdot 9\cdot 8}\\[5pt]&=&\frac{5}{6} \end{eqnarray}$$

余弦定理での計算は、約分できる可能性が高いので分母にある\(2\cdot 9\cdot 8\) は計算せずにそのままにしておいた方がいいですね(^^)

このように\(\cos\) の値が求まったら、三角比の相互関係である\(\sin^2\theta+\cos^2\theta=1\) を用いて\(\sin\) の値を求めます。

$$\begin{eqnarray}\sin^2 A+\left(\frac{5}{6}\right)^2&=&1\\[5pt]\sin^2 A&=&1-\frac{25}{36}\\[5pt]\sin^2 A &=&\frac{11}{36} \\[5pt]\sin A>0&\color{white}{=}&だから\\[5pt]\sin A&=& \frac{\sqrt{11}}{6}\end{eqnarray}$$

これでようやく面積公式に必要な\(\sin\) の値を求めることができたので

$$\begin{eqnarray}S&=&\frac{1}{2}bc\sin A\\[5pt]&=&\frac{1}{2}\cdot 8\cdot 9\cdot \frac{\sqrt{11}}{6}\\[5pt]&=&6\sqrt{11}\end{eqnarray}$$

んー、長い道のりでしたが

角度が分からない場合には、余弦定理で\(\cos\)を求める。

三角比の相互関係を使って\(\sin\) に変換する。

ここかでようやく面積公式を使う。

このような流れでやっていきましょう。

とはいえ…もうちょっとラクにやる方法ってないんですかねぇ？

っていう方の願いをかなえるため

3辺の長さしか与えられなかった場合に、簡単に面積を求める特別な公式について次の章でお話していきます。

【三角比の面積】ヘロンの公式を使った計算

ヘロンの公式というものを使うと、3辺の長さしか分からない場合でも簡単に三角形の面積を求めることができます。

ヘロンの公式

\(\displaystyle{s=\frac{a+b+c}{2}}\) とすると

$$S=\sqrt{s(s-a)(s-b)(s-c)}$$

え、ナニコレ

めっちゃ複雑なんだけど…

って思いがちですが、実際に使ってみるとすごく簡単に感じると思います。

ってわけで、先ほどの章で解いた問題をヘロンの公式を用いて計算してみましょう。

まず、\(s\)となる値を求めます。

$$s=\frac{5+9+8}{2}=11$$

この\(s\)を用いて、ヘロンの公式に当てはめていきます。

$$\begin{eqnarray}S&=&\sqrt{s(s-a)(s-b)(s-c)}\\[5pt]&=&\sqrt{11(11-5)(11-9)(11-8)}\\[5pt]&=&\sqrt{11\cdot 6\cdot 2\cdot 3}\\[5pt]&=&6\sqrt{11}\end{eqnarray}$$

このように計算することができました！

ヘロンの公式を使えば、あっという間に答えを出すことができますね。

先ほどは余弦定理や相互関係などを駆使しながら、たくさんの計算を経て面積を求めました。

だけど、ヘロンの公式を覚えておけばこんなにもあっさりと…

ということで、ヘロンの公式は覚えておいて損はないかと思います(^^)

【三角比の面積】四角形の面積を求める計算

次は、四角形の面積を求める問題についてみていきましょう。

三角比の単元では、次のような円に内接する四角形を扱うことが多いです。

このような四角形は、どのように面積を求めればよいのでしょうか、考えていきましょう！

【三角比の面積問題】

四角形ABCDが円に内接し、\(AB=1\), \(BC=2\), \(CD=2\), \(DA=3\) であるとき、四角形ABCDの面積を求めなさい。

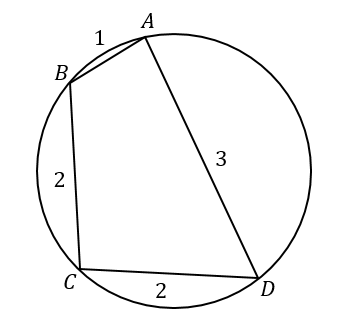
四角形の面積を考える場合には

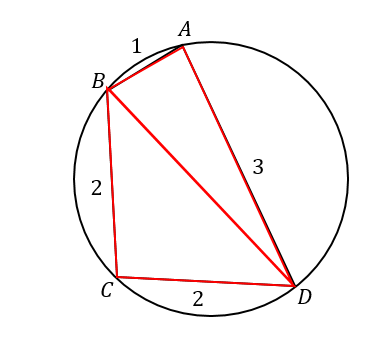
このように補助線を引き、2つの三角形に分けます。

そして、それぞれの三角形の面積を求めて、合計すればよいと考えていきます。

まず、△ABCに注目していきます。

角Aを基準に余弦定理を使うと、次のような式ができます。

$$\begin{eqnarray}BD^2&=&1^2+3^2-2\cdot 1\cdot 3\cos A\\[5pt]&=&10-6\cos A \end{eqnarray}$$

次に、△BCDにおいて角Cを基準に余弦定理を使うと、次のような式ができます。

$$\begin{eqnarray}BD^2&=&2^2+2^2-2\cdot 2\cdot 2\cos C\\[5pt]&=&8-8\cos C \end{eqnarray}$$

内接する四角形の対角の和は180°になるので、\(C=180°-A\) と表すことができ

$$\cos C=\cos (180°-A)=-\cos A$$

となります。

よって

$$\begin{eqnarray}BD^2&=&8-8\cos C \\[5pt]&=&8+8\cos A\end{eqnarray}$$

以上より、\(BD^2\)の式を2つ作ることができたので、それらをイコールでつなぐと

$$\begin{eqnarray}10-6\cos A &=& 8+8\cos A\\[5pt]-14\cos A&=&-2\\[5pt]\cos A&=&\frac{1}{7}\end{eqnarray}$$

\(\cos\) の値が分かれば、相互関係を使って\(\sin\)を求めます。

$$\begin{eqnarray}\sin^2 A+\left(\frac{1}{7}\right)^2&=&1\\[5pt]\sin^2 A&=&1-\frac{1}{49}\\[5pt]\sin^2 A&=&\frac{48}{49}\\[5pt]\sin A&=&\frac{4\sqrt{3}}{7} \end{eqnarray}$$

\(\sin\) の値が求まったら、それぞれの三角形の面積を求めることができます。

$$\begin{eqnarray}△ABCの面積&=&\frac{1}{2}\cdot 1\cdot 3\cdot \frac{4\sqrt{3}}{7}\\[5pt]&=&\frac{6\sqrt{3}}{7} \end{eqnarray}$$

$$\begin{eqnarray}△BCDの面積&=&\frac{1}{2}\cdot 2\cdot 2\cdot \frac{4\sqrt{3}}{7}\\[5pt]&=&\frac{8\sqrt{3}}{7} \end{eqnarray}$$

よって、四角形の面積は

$$\begin{eqnarray}四角形ABCDの面積&=&\frac{6\sqrt{3}}{7}+\frac{8\sqrt{3}}{7}\\[5pt]&=&\frac{14\sqrt{3}}{7}\\[5pt]&=&2\sqrt{3} \end{eqnarray}$$

このように内接している四角形では、2つの三角形に分けることで面積を求めることができます。

また、内接している四角形においては、対角の和が180°になるということから

このような変形を用いていくことになるので、頭に入れておいてくださいね(^^)

【三角比の面積】まとめ！

お疲れ様でした！

最後に、三角比を用いた三角形の面積を公式を確認しておきましょう。

三角比の面積公式

$$\begin{eqnarray}S&=&\frac{1}{2}bc\sin A\\[5pt]&=&\frac{1}{2}ca\sin B\\[5pt]&=&\frac{1}{2}ab\sin C \end{eqnarray}$$

ヘロンの公式

\(\displaystyle{s=\frac{a+b+c}{2}}\) とすると

$$S=\sqrt{s(s-a)(s-b)(s-c)}$$