高校数学Ⅰで学習する三角比の単元から
「三角比を含む方程式の解き方」
について解説していきます。
この記事は、数学がニガテ…という方に向けて解き方の手順をイチから解説していきます。
以下の問題を取り上げて、それぞれの解き方、考え方についてまとめていきます。
【問題】
\(0°≦\theta≦180°\) のとき,次の式を満たす \(\theta\) を求めよ。
(1)\(\sin \theta \frac{1}{\sqrt{2}}\)
(2)\(\cos \theta =\frac{\sqrt{3}}{2}\)
(3)\(\tan \theta=-1\)
三角比を含む方程式を解くには、単位円(半径1の円)を使って考えるのが基本です。
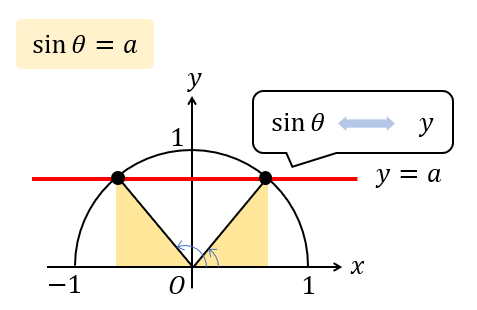
\(\sin \theta =a\) ならば、\(y=a\) の直線を引き、単位円との交点を求めて角度を求める。
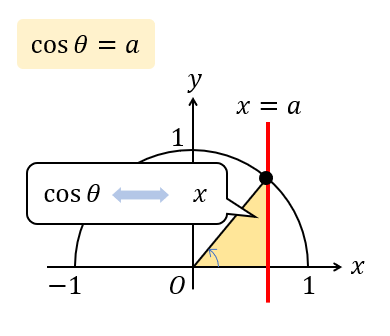
\(\cos \theta =a\) ならば、\(x=a\) の直線を引き、単位円との交点を求めて角度を求める。
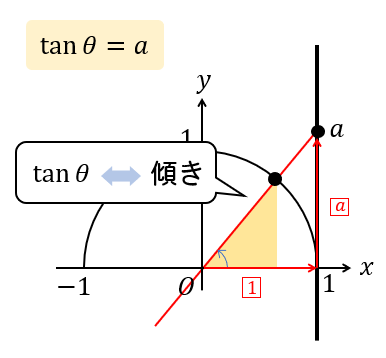
\(\tan \theta =a\) ならば、原点を通る傾きが \(a\) の直線を引き、単位円との交点を求めて角度を求める。
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
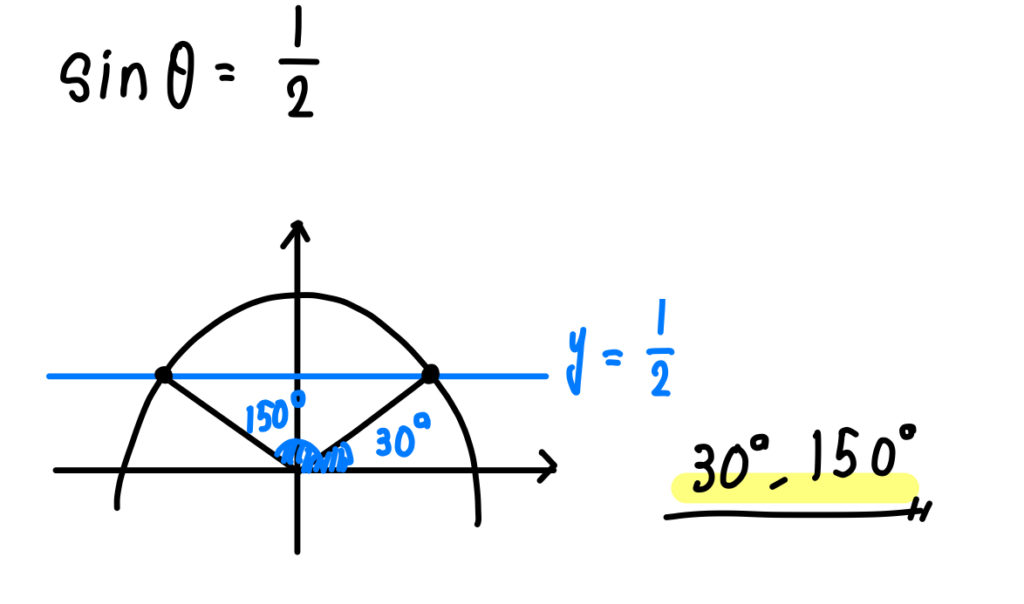
三角比を含む方程式【sin】
\(0°≦\theta≦180°\) のとき,次の式を満たす \(\theta\) を求めよ。
(1)\(\sin \theta \frac{1}{\sqrt{2}}\)
まずは半径1の半円をかきます。
そこに、\(y=\frac{1}{\sqrt{2}}\) となる直線(横線)を書き入れます。
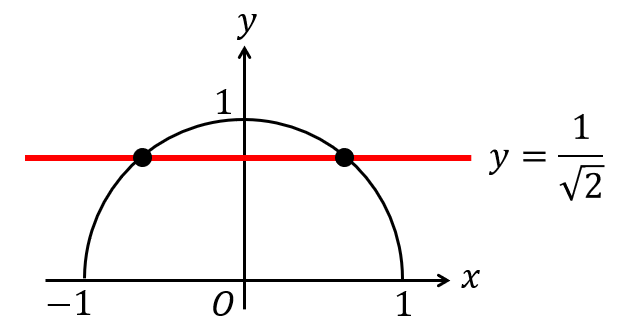
このとき、線を引く位置はなるべく正確にしておいた方が角を求めるときの判断に役立ちます。
\(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{1.4\cdots}{2}=0.7\cdots\)
ということで、半分よりもちょっと上くらいのところに横線を引けばある程度、正確な位置に引くことができますね。
そして、この直線と単位円が交わる点に注目して角度を求めていきます。
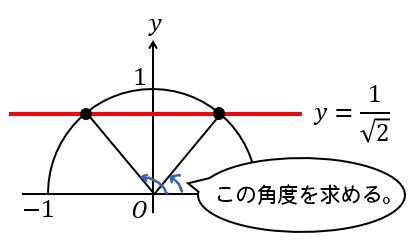
このとき、\(\sin45°\) が \(\frac{1}{\sqrt{2}}\) になるのということを覚えている人は話が早いです。
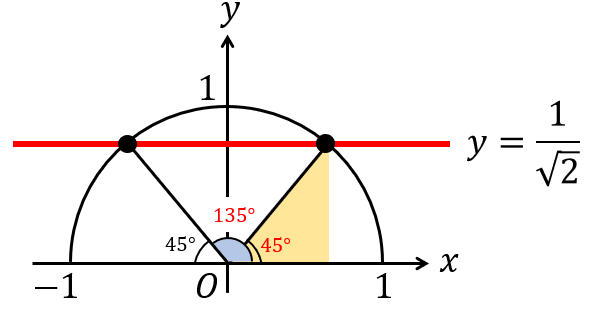
2つの点は \(y\) 軸に関して対称な位置にあるので、
\(45°,135°\) になるということが分かります。
すぐにパッと角度が出てこない…という方は
三角形を取り出してみて、直角三角形の辺の比から角度を考えてみてください。
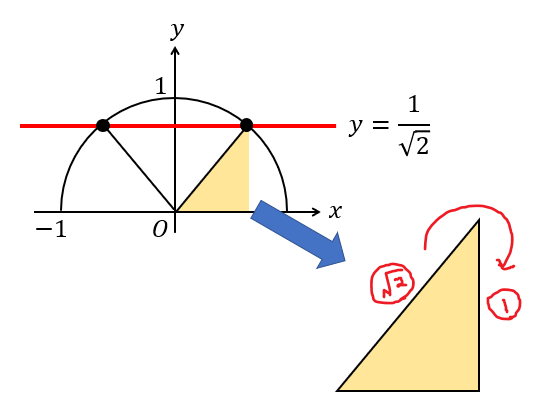
\(\sin\) の位置関係のところに\(\sqrt{2}\)、\(1\) を書き入れてみると、
\(1:1:\sqrt{2}\) の直角三角形で45°の角になることが分かりますね。
答え
$$45°,135°$$
三角比を含む方程式【cos】
\(0°≦\theta≦180°\) のとき,次の式を満たす \(\theta\) を求めよ。
(2)\(\cos \theta =\frac{\sqrt{3}}{2}\)
まずは半径1の半円をかきます。
そこに、\(x=\frac{\sqrt{3}}{2}\) となる直線(縦線)を書き入れます。
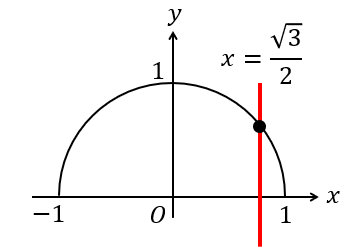
\(\frac{\sqrt{3}}{2}=\frac{1.7\cdots}{2}=0.8\cdots\)
ということで、1に近いところに線を引けばある程度、正確に引くことができますね。
\(\sin\) のときは違って、単位円との交点は1点しかありません。
なので、求める角はこの部分だけでOKです。
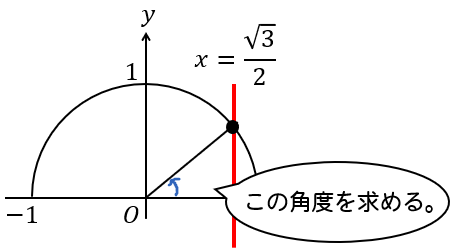
というわけで、\(\cos30°\) が \(\frac{\sqrt{3}}{2}\) になるのということを覚えていれば
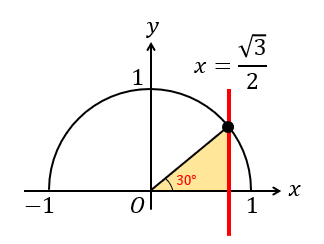
答えは30°であることがすぐに分かります。
覚えていない…という方は、

\(\cos\) の位置関係のところに\(2\)、\(\sqrt{3}\) を書き入れてみると、
\(1:2:\sqrt{3}\) の直角三角形で30°の角になることが分かりますね。
答え
$$30°$$
三角比を含む方程式【tan】
\(0°≦\theta≦180°\) のとき,次の式を満たす \(\theta\) を求めよ。
(3)\(\tan \theta=-1\)
まずは半径1の半円をかきます。
そこに、傾きが \(-1\) で原点を通る直線を書き入れます。
傾き \(-1\) というのは、1進むと1下がる直線のことですので、次のような形になります。
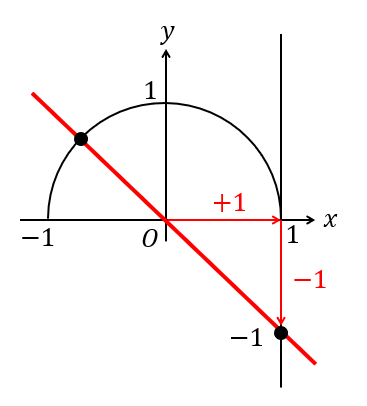
そして、単位円との交点に注目して角度を求めればよいので
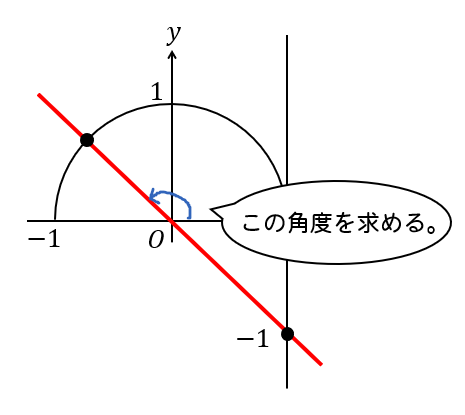
ここの部分を求めていくことになります。
角の大きさが鈍角になっているので、ちょっと読み取りづらいですね。
そういう場合には、
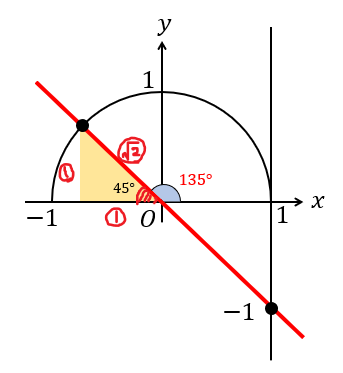
ここの三角形に注目して角度を求めてみましょう。
すると、その隣にある角は \(135°\) になるってことがわかりますね。
答え
$$135°$$
練習問題に挑戦!
【問題】
\(0°≦\theta≦180°\) のとき,次の式を満たす \(\theta\) を求めよ。
(1)\(\sin \theta \frac{1}{2}\)
(2)\(\cos \theta =-\frac{\sqrt{3}}{2}\)
(3)\(\tan \theta=\sqrt{3}\)
まとめ!
お疲れ様でした!
三角比を含む方程式は理解できましたか??
慣れるまでは難しいかもしれませんが、たくさん問題を解きながら単位円と交点との関係をマスターしていきましょう。
まずは、以下のポイントをおさえておいてくださいね!
- \(\sin\) ⇒ \(y\)
- \(\cos\) ⇒ \(x\)
- \(\tan\) ⇒ 傾き


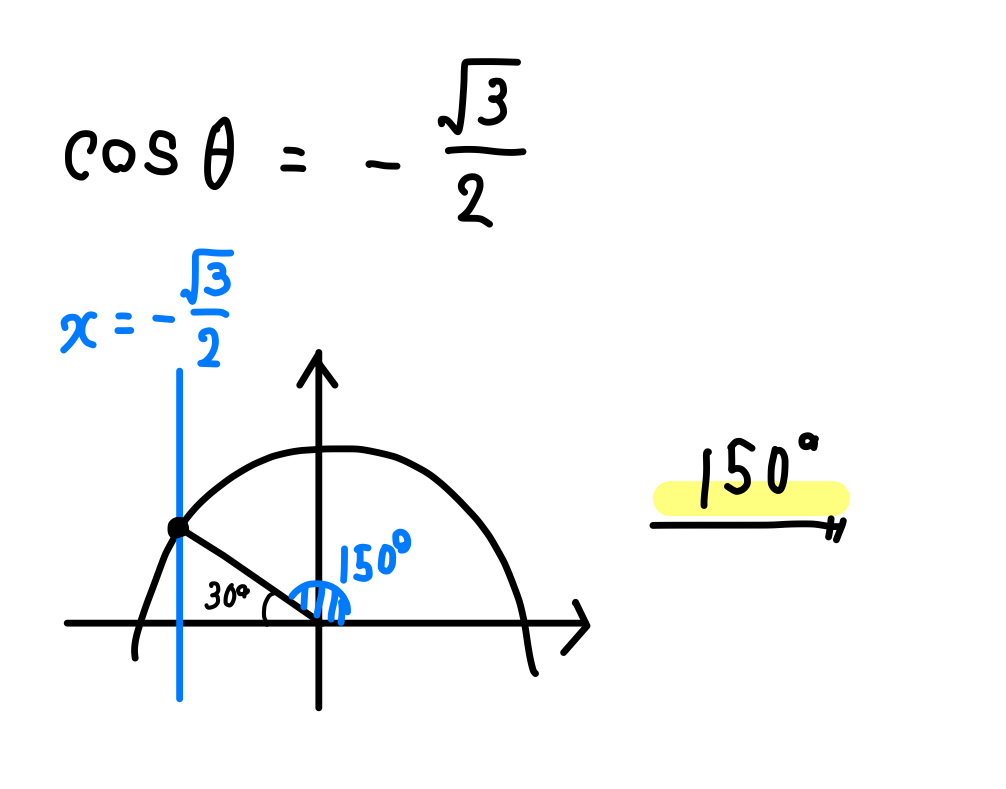















コメントを残す