三角形の面積を求めたいとき
3辺の長さが分かっている場合には
ヘロンの公式を使うとラクに計算ができるようになります。
ヘロンの公式
\(\displaystyle{s=\frac{a+b+c}{2}}\) とすると
$$S=\sqrt{s(s-a)(s-b)(s-c)}$$
こちらの動画内でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
ヘロンの公式の使い方
では、ヘロンの公式の使い方について確認していきましょう。
公式がちょっと複雑に見えるのですが、手順を覚えてしまえば簡単です(^^)
【問題】
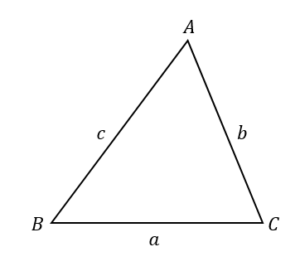
次のような△ABCの面積を求めなさい。
$$a=5, b=9, c=8$$

ヘロンの公式を使うためには、\(s\)の値を求めるという準備が必要です。
\(\displaystyle{s=\frac{a+b+c}{2}}\) にそれぞれの辺の大きさを代入しましょう。
$$\begin{eqnarray}s&=&\frac{5+9+8}{2}\\[5pt]&=&\color{red}{11} \end{eqnarray}$$
\(s\)の値が求まったら準備完了です。
の中にそれぞれの値を代入していきましょう。
$$\begin{eqnarray}S&=&\sqrt{s(s-a)(s-b)(s-c)}\\[5pt]&=&\sqrt{11(11-5)(11-9)(11-8)}\\[5pt]&=&\sqrt{11\cdot 6\cdot 2\cdot 3}\\[5pt]&=&6\sqrt{11}\cdots(解)\end{eqnarray}$$
このように計算することができます。
公式の形を覚える必要がありますが、かなり時短になると思います。
以下では、ヘロンの公式を使わずに面積を求める手順についても紹介しておきます。
ヘロンの公式を使った場合がいかにラクだったかを実感してくださいな。
次のような△ABCの面積を求めなさい。
$$a=5, b=9, c=8$$
ヘロンの公式を使わない場合、\(S=\frac{1}{2}bc\sin A\)の公式を用いて求めます。
ただ…問題文には\(\sin A\)の値が与えられていないので、準備として自分で計算しておく必要があります。
角Aに注目して、余弦定理を使うと
$$\begin{eqnarray}\cos A&=&\frac{9^2+8^2-5^2}{2\cdot 9\cdot 8}\\[5pt]&=&\frac{120}{2\cdot 9\cdot 8}\\[5pt]&=&\frac{5}{6} \end{eqnarray}$$
これにて、\(\cos A\)の値が求まりました。ここから\(\sin A\)に変換していきましょう。
三角比の相互関係である\(\sin^2\theta+\cos^2\theta=1\) を用いると
$$\begin{eqnarray}\sin^2 A+\left(\frac{5}{6}\right)^2&=&1\\[5pt]\sin^2 A&=&1-\frac{25}{36}\\[5pt]\sin^2 A &=&\frac{11}{36} \\[5pt]\sin A>0&\color{white}{=}&だから\\[5pt]\sin A&=& \frac{\sqrt{11}}{6}\end{eqnarray}$$
これでようやく\(\sin A\)の値が求まったので、面積の公式\(S=frac{1}{2}bc\sin A\)に当てはめていきましょう。
$$\begin{eqnarray}S&=&\frac{1}{2}bc\sin A\\[5pt]&=&\frac{1}{2}\cdot 8\cdot 9\cdot \frac{\sqrt{11}}{6}\\[5pt]&=&6\sqrt{11}\cdots(解)\end{eqnarray}$$
んー、計算が長い!!
こちらの解法も大切ではあるんだけど、
実力がついてきて、こんな問題は楽勝だぜ!っていうかたはヘロンの公式を使って時短していきましょう。
まだまだ余弦定理や三角形の面積の公式を覚えきれていない人は、練習のためにはこちらの面倒なやり方でやるのがいいですね。
ヘロンの公式の証明
では、なぜこのような公式で面積を求めることができるのか。
その証明方法について確認しておきましょう。
証明はちょっと複雑な式変形を伴います。
オレは公式が使えたらそれで十分だぜ!っていう方は次の章にある練習問題にお進みください。
〈証明〉
\(S=\frac{1}{2}bc\sin A\)の形からスタートします。
$$\begin{eqnarray}\frac{1}{2}bc\sin A&=&\frac{1}{2}bc\sqrt{1-\cos^2 A}\\[5pt]&=&\frac{1}{2}bc\sqrt{1-\left(\frac{b^2+c^2-a^2}{2bc}\right)^2}\\[5pt]&=&\frac{1}{2}bc\cdot \frac{1}{2bc}\sqrt{(2bc)^2-(b^2+c^2-a^2)^2}\\[5pt]&=&\frac{1}{4}\sqrt{\{(b+c)^2-a^2\}\{a^2-(b-c)^2\}}\\[5pt]&=&\frac{1}{4}\sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)} \end{eqnarray}$$
ここまできたら、\(a+b+c=s\)とおきます。すると
$$b+c-a=a+b+c-2a=2s-2a$$
$$a+b-c=a+b+c-2c=2s-2c$$
$$a-b+c=a+b+c-2b=2s-2b$$
となるので、次のように変形することができます。
$$\begin{eqnarray}&&\frac{1}{4}\sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}\\[5pt]&=&\frac{1}{4}\sqrt{2s(2s-2a)(2s-2b)(2s-2c)}\\[5pt]&=&\frac{1}{4}\cdot4\sqrt{s(s-a)(s-b)(s-c)}\\[5pt]&=&\sqrt{s(s-a)(s-b)(s-c)} \end{eqnarray}$$
以上!
長かったですが、ヘロンの公式はこのように導くことができます。
ヘロンの公式の計算練習
次のような△ABCの面積を求めなさい。
$$a=7, b=8, c=13$$
次のような△ABCの面積を求めなさい。
$$a=6, b=5, c=4$$
まとめ!
ヘロンの公式

\(\displaystyle{s=\frac{a+b+c}{2}}\) とすると
$$S=\sqrt{s(s-a)(s-b)(s-c)}$$
というわけで、今回はヘロンの公式の使い方についてサクッと解説しました。
ちょっとね、見た目が難しそうなので
初めは覚えるのが大変だとは思います。
しかし、使いこなせるようになるとすっごく便利です。
入試でもヘロンの公式が使えた方がやっぱり強いですよ(^^)
さぁ、練習してしっかりと身につけておきましょう(/・ω・)/
















コメントを残す