こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する式と証明の単元から「二項定理を用いた証明」について取り上げます。
難しい問題に見えますが、ポイントをおさえてしまえば数学を苦手にしている方でもサクッと解けるようになっちゃいますから、今回の記事を通して、しっかりと理解を深めていきましょう!
今回取り上げる問題はこちらです。


サクッと理解したい方は、こちらの動画も参考にしてください!
メルマガ講座の中でYouTube講義のまとめサイトをお渡ししています。まとめサイトには動画講義のほか、定期テスト対策の特訓課題なども収録しているのでぜひご活用ください。無料で登録できるのでこちらからお願いします^^
証明のポイント!展開式を作れるようにしておく
今回の証明をクリアするためには、\((1+x)^n\)の展開式を用意しておくことがポイントです。

二項定理を用いて展開しただけですね!
ただ、よく使うものになるのでこの形を覚えておけると理想的です^^
そして、この式を作っておいたらそれぞれの証明にとりかかっていきましょう。
等式の証明
(1)の解説

先ほど作っておいた展開式の\(1+x\)の部分と、証明したい等式の\(-2\)の部分を見比べます。
そして、\(x\)に何を代入すればいいかを見つけましょう。
すると、\(1+x=-2\) を解くことで、\(x=-3\) が見つかりますね!
これを見つけたら、準備で作っておいた展開式の中に\(-3\)を代入します。そうすると、証明したかった等式を導くことができますね^^
\(x\)に何を代入すればよいか見つける → 代入してみる → 証明したかった等式ができあがり!
たったこれだけのことです^^
それでは続けて問題を見ていきましょう。
(2)の解説

(1)の解き方が理解できていれば、こちらも問題なく理解できるでしょう!
(3)の解説

分数なので少し戸惑ってしまいますが、\(1+x=\frac{1}{2}\) を解けば、\(x\)の値もすぐに見つかりますね!
\(x\)を代入した後の式変形ややこしく感じるかもしれませんが
\((-\frac{1}{2})^2=\frac{(-1)^2}{2^2}=\frac{1}{2^2}\)
\((-\frac{1}{2})^n=\frac{(-1)^n}{2^n}\)
このように変形している感じですね!
(4)の解説 nが奇数のパターン

今までの等式と見た目が異なっているので、困ってしまった人が多いと思います。
ですが、やることは一緒です!!上の画像にあるように、右辺をすべて左辺に移項してしまえばいいですね。
\((-1)^{偶数}=1\)
\((-1)^{奇数}=-1\)
となることにも注意しながら式を変形していけば完成です^^
不等式の証明
(1)の解説

まずは\((1+\frac{1}{n} )^n\)の展開式をつくりましょう。
最初に用意しておいた\((1+x)^n\)の\(x\)の部分が\(\frac{1}{n}\)になっただけですから、かんたんにつくれますよね!
次に、\(C\)の計算や\(\frac{1}{n}\)が正であることから、上の画像の赤マーカー部分を取り除いてやると、等式の関係がくずれて左辺の方が大きい不等式にすることができます。
ここの変形がしっくりこない方は、重さがつり合っている天秤をイメージしましょう。そこから片方の重りを取り除くと、つり合いが崩れてしまって、もう一方のお皿が重たくなりますよね。これを同じ事をやっている感じです!
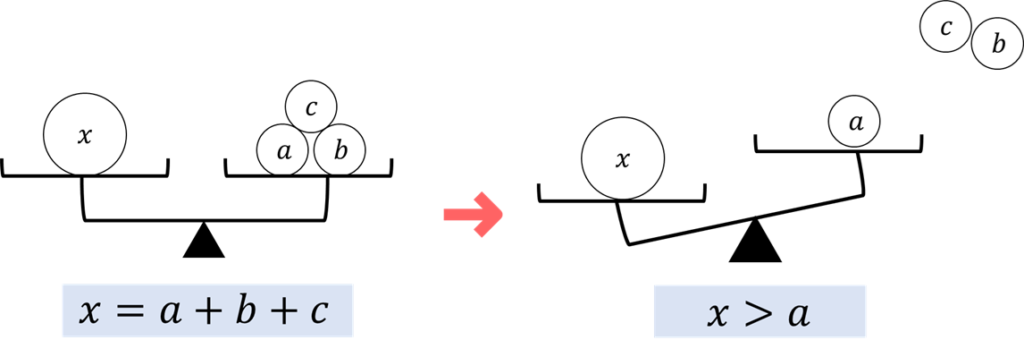
すると、あとは計算を進めていくことで証明したかった不等式を導くことができます。
(2)の解説

これも(1)とやることは同じです。
展開式を作ったら、上の画像の赤マーカー部分を取り除いて不等式をつくっちゃいましょう。
どの部分を取り除けばいいのかは、与えられている不等式の形を見ながら判断してください。
今回は証明したい不等式の右辺に項が3つあるので、\((1+x)^n\)の展開式のうち3つの分の項を残して、それ以外を取り除くように判断しています。
まとめ
お疲れさまでした!
これで二項定理による等式、不等式の証明はバッチリですかね^^
ここでのポイントは次の展開式を作れるようになることですね!
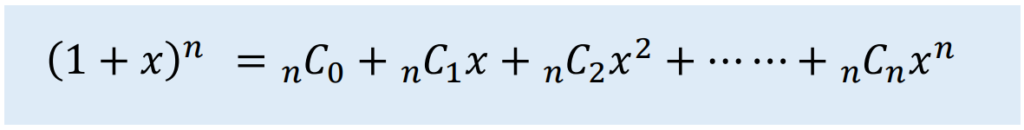
これさえできてしまえば、あとは単純な計算だけでOKですから。
テストでしっかりと得点できるように特訓しておきましょう!
それでは今回は以上!
こちらの記事ではテスト頻出の問題も解説しているので、チェックしといてください(‘ω’)ノ
















コメントを残す