高校数学Aで学習する整数の性質から
「分数形の不定方程式の解き方」
についてイチから解説していきます。
分数形の不定方程式には、
文字が2種類のとき、3種類のときの2パターンがあります。
どちらも質問が多い問題なので、解き方と考え方をこちらの記事でまとめておきますね!
【問題】
(文字が2種類のパターン)
\(\frac{1}{x}+\frac{2}{y}=1\) を満たす整数 \(x, \ y\)の組をすべて求めよ。
(文字が3種類のパターン)
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\) \((x≧y≧z)\) を満たす自然数 \(x, \ y, \ z\)の組をすべて求めよ。
こちらの動画でも解説しているので参考にしてみてください^^
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
分数形の不定方程式(文字が2種類)
【問題】
\(\frac{1}{x}+\frac{2}{y}=1\) を満たす整数 \(x, \ y\)の組をすべて求めよ。
文字が2種類のときは、分母の最小公倍数を両辺にかけて分数の形を消す。
そして、通常の不定方程式と同じ形に変形してやることがポイントです。
それと、注意しておきたいのが
分母にある\( x, \ y\) はともに0にはならないということですね。
計算の過程で\(x=0 , \ y=0\) となることがあれば、それは不適ということになります。

途中で共通因数をくくるために、
無理やり「\(+2, \ -2\)」を持ってきている辺りが難しく感じるかもしれません(^^;)
\(x\) でくくったときにでてきた\((y-2)\)と同じになるように数字を作っています。
ここは慣れが大事なので、たくさんの問題を解いて慣れていきましょう。
分数形の不定方程式(文字が3種類)
【問題】
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\) \((x≧y≧z)\) を満たす自然数 \(x, \ y, \ z\)の組をすべて求めよ。
文字が3種類のときには、それぞれの文字に「自然数」「大小関係」といった条件が与えられていることがほとんどです。
この条件を用いて、ある文字の範囲を絞っていくというのがポイントとなります。
\(x,y,z\) の中で最も小さい値をとる\( z \)に着目して、次のように範囲を絞っていきます。

さて、これはどんな変形をしたのか理解できますか?
ここは質問をいただくことの多い場面ですので、丁寧に解説しておきますね。
\(\frac{1}{x}≦\frac{1}{z}\) , \(\frac{1}{y}≦\frac{1}{z}\) だから、
それぞれの部分を \(z\) を使った式で書き換えると次のように文字を \(z\) だけに統一することができます。
ここから \(z≦3\) であり、\(z\) は自然数であることから
\(z=1, \ 2, \ 3\) になるってことがわかります。
このようにまずは、ある文字に着目して範囲を絞っていくようにしましょう。
すると、ここから\(z\)の場合分けを利用しながら\(x, \ y\)の値を探っていきましょう。
\(z=1\) のとき
$$\begin{eqnarray}\frac{1}{x}+\frac{1}{y}+1&=&1\\[5pt]\frac{1}{x}+\frac{1}{y}&=&0 \end{eqnarray}$$
\(0<\frac{1}{x}≦\frac{1}{y}\) だから、この式を満たす自然数\(x , y\) は存在しません。
よって、\(z=1\) のときは不適となります。
\(z=2\) のとき
$$\begin{eqnarray}\frac{1}{x}+\frac{1}{y}+\frac{1}{2}&=&1\\[5pt]\frac{1}{x}+\frac{1}{y}&=&\frac{1}{2} \end{eqnarray}$$
ここから \(y\)に着目して、範囲を絞っていきましょう。
$$\begin{eqnarray}\frac{1}{2}=\frac{1}{x}+\frac{1}{y}≦\frac{1}{y}+\frac{1}{y}=\frac{2}{y} \end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{2}&≦&\frac{2}{y}\\[5pt]y&≦&4\\[5pt]2=z≦y&≦&4 \end{eqnarray}$$
よって、\(y=2,3,4\) に絞ることができます。
\(y=2, \ z=2\) のとき
$$\begin{eqnarray}\frac{1}{x}+\frac{1}{2}&=&\frac{1}{2}\\[5pt]\frac{1}{x}&=&0 \end{eqnarray}$$
となり、\(0<\frac{1}{x}\) だから、これを満たす自然数\(x\) はない。
次に、\(y=3, \ z=2\) のとき
$$\begin{eqnarray}\frac{1}{x}+\frac{1}{3}&=&\frac{1}{2}\\[5pt]\frac{1}{x}&=&\frac{1}{6}\\[5pt]x&=&6 \end{eqnarray}$$
よって、\(x=6, \ y=3, \ z=2\) は答えとしてOK。
次に、\(y=4, \ z=2\) のとき
$$\begin{eqnarray}\frac{1}{x}+\frac{1}{4}&=&\frac{1}{2}\\[5pt]\frac{1}{x}&=&\frac{1}{4}\\[5pt]x&=&4 \end{eqnarray}$$
よって、\(x=4, \ y=4, \ z=2\) は答えとしてOK。
また \(z\) の場合分けに戻って
\(z=3\) のとき
$$\begin{eqnarray}\frac{1}{x}+\frac{1}{y}+\frac{1}{3}&=&1\\[5pt]\frac{1}{x}+\frac{1}{y}&=&\frac{2}{3} \end{eqnarray}$$
ここから \(y\)に着目して、範囲を絞っていきましょう。
$$\begin{eqnarray}\frac{2}{3}=\frac{1}{x}+\frac{1}{y}≦\frac{1}{y}+\frac{1}{y}=\frac{2}{y} \end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{3}&≦&\frac{2}{y}\\[5pt]y&≦&3\\[5pt]3=z≦y&≦&3 \end{eqnarray}$$
よって、\(y=3\) に絞ることができます。
\(y=3, \ z=3\) のとき
$$\begin{eqnarray}\frac{1}{x}+\frac{1}{3}&=&\frac{2}{3}\\[5pt]\frac{1}{x}&=&\frac{1}{3}\\[5pt]x&=&3 \end{eqnarray}$$
よって、\(x=3, \ y=3, \ z=3\) は答えとしてOK。
以上より、
\(\color{red}{(x,y,z)=(6,3,2)(4,4,2)(3,3,3)}\) が答えとなります。
また、文字が3種類のときには、次のように「自然数」という条件だけで解く問題もあります。
参考程度に解き方を載せておきますね(^^)
【問題】
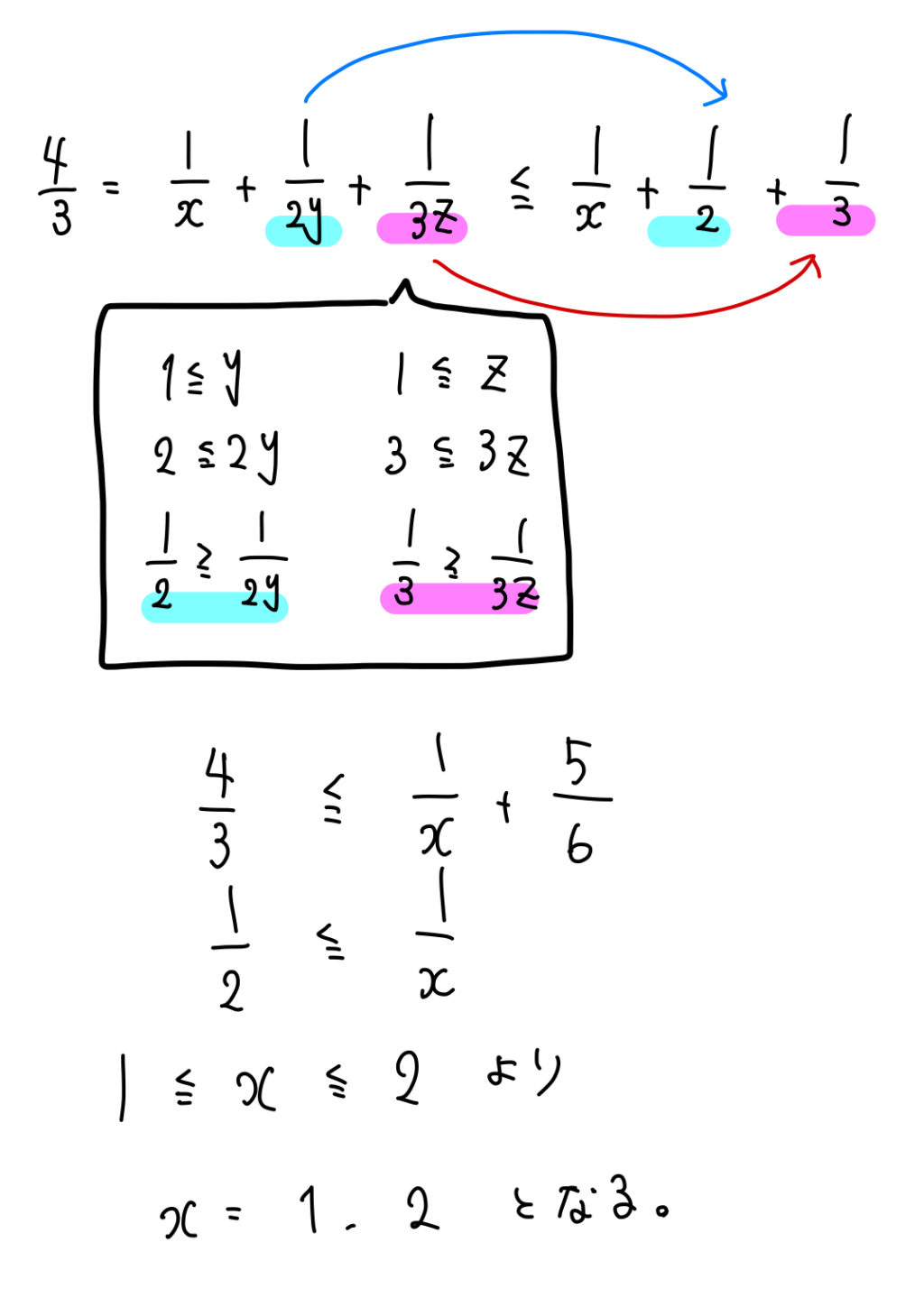
\(\frac{1}{x}+\frac{1}{2y}+\frac{1}{3z}=\frac{4}{3}\) を満たす自然数 \(x, \ y, \ z\)の組をすべて求めよ。


まとめ!
お疲れさまでした!
分数形の不定方程式では、
- 文字が2種類なら分数を消す!
- 文字が3種類なら文字を1つに減らして範囲を絞る!
というのが考え方になります。
たくさん練習問題を解いて理解を深めておきましょう(/・ω・)/















分かりやすい説明ありがとうございます。
1つ分からないところがあり質問します。
文字が3種類の所の以下の部分ですが
3=z≦y≦4
なぜ
3ではなく4なのでしょうか。
その上の式では
y≦4
となっているのに、です。
基本的なことかもしれませんが、よろしくお願いします。
コメントありがとうございます!
ご指摘いただいたように、
3=z≦y≦4の部分は
正しくは3=z≦y≦3となり
y=3だけに絞られます。
こちらのミスでお恥ずかしい限りです…
混乱させてしまい申し訳ありませんでした。
ご指摘ありがとうございます。