今回は高校数学Ⅱで学習する微分の単元から
「接線の方程式を求める」
について、パターン別に解説していきます。
覚えておきたいのは次の3パターンになります。
【接点が分かってる基本パターン】
関数\(y=x^2-2x+3\)上の点\((2,3)\)における接線の方程式を求めよ。
【傾きが分かってるパターン】
関数\(y=x^3\)において,傾きが\(3\)である接線の方程式を求めよ。
【接点が分からないパターン】
点\((1,0)\)から、放物線\(y=x^2+3\)に引いた接線の方程式を求めよ。
ポイントとしては…
接線の傾きは微分で求める!
ということですね。
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
接線の方程式【接点分かってるパターン】
【接点が分かってる基本パターン】
関数\(y=x^2-2x+3\)上の点\((2,3)\)における接線の方程式を求めよ。
それでは、接線の方程式を求める手順を確認しましょう。
まずは、関数の式を微分して、接点の\(x\)座標を代入。

すると、接線の傾きを求めることができます。
ここで絶対に覚えておきたいのが
微分した式に接点の\(x\)座標を代入すると、傾きが求まる。
ということです。
傾きが求まったことで、今回の接線の方程式は
傾きが\(2\)で、点\((2,3)\)を通る直線の式
であることが分かります。
ここまで来たら、
あとは直線の式の公式に当てはめていけばOKですね。
傾き\(a\)、点\((p,q)\)を通る直線の式
$$y-q=a(x-p)$$

公式に当てはめることができたら
計算をすすめて、\(y=\cdots\)の形にしていけば完成です。
$$\begin{eqnarray}y-3&=&2(x-2)\\[5pt]y&=&2x-4+3\\[5pt]y&=&2x-1\cdots(解) \end{eqnarray}$$
イメージとしてはこんな感じです。
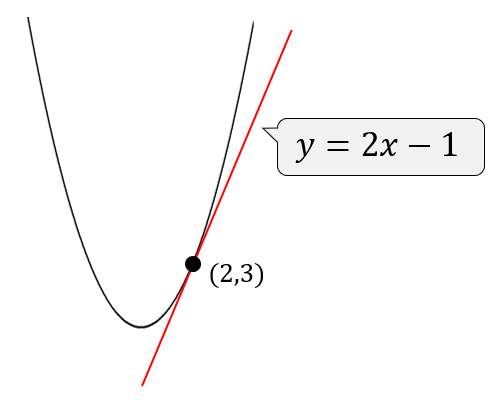
答え
$$y=2x-1$$
接線の方程式【傾き分かってるパターン】
【傾きが分かってるパターン】
関数\(y=x^3\)において,傾きが\(3\)である接線の方程式を求めよ。
今回の問題では、傾きが与えられていますが
接点が分からなくなっています…。
接線の式を求めるためには
先ほどの問題でやったように、
接点と傾きが必要になります。
というわけで、まずは接点を求めていきましょう。
微分した式が\(3\)になるところ、それが今回の接点の\(x\)座標となります。

\(x\)座標が分かれば、\(f(x)\)に代入することで\(y\)座標も求めることができます。
\(f(1)=1^3=1\)、よって接点は\((1,1)\)。
\(f(-1)=(-1)^3=-1\)、よって接点は\((-1,-1)\)。
このように2つの接点を求めることができました。
これで接点と傾きが揃ったので、
接線の方程式を作っていくことができます。
傾き\(3\)、接点\((1,1)\)だから
$$\begin{eqnarray}y-1&=&3(x-1)\\[5pt]y&=&3x-3+1\\[5pt]y&=&3x-2\cdots(解) \end{eqnarray}$$
傾き\(3\)、接点\((-1,-1)\)だから
$$\begin{eqnarray}y-(-1)&=&3\{x-(-1)\}\\[5pt]y&=&3x+3-1\\[5pt]y&=&3x+2\cdots(解) \end{eqnarray}$$
イメージとしてはこんな感じです。
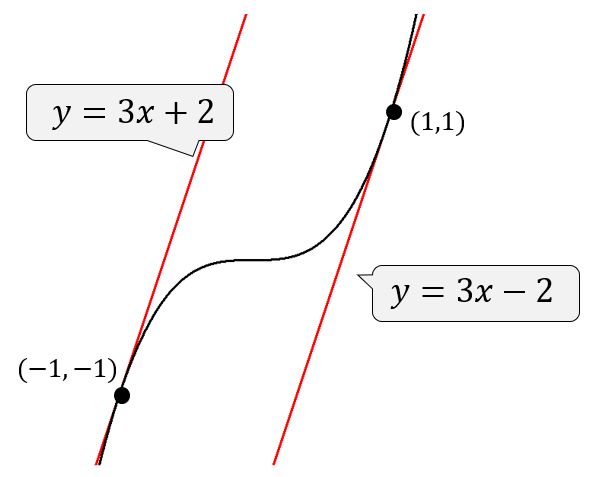
傾きが分かれば、そこから接線を求めることもできる。
これを覚えておきましょう!
答え
$$y=3x-2$$
$$y=3x+2$$
接線の方程式【接点分かってないパターン】
【接点が分からないパターン】
点\((1,0)\)から、放物線\(y=x^2+3\)に引いた接線の方程式を求めよ。
最後は、接点も傾きも分っていないパターンの問題です。
計算式が長くなることから、テストでも大問として出題されることが多い問題です。
でも…点\((1,0)\)って書いてあるから
これが接点じゃないの??
と、勘違いしてしまいそうになるのですが
今回の問題では「グラフ上の点」とはどこにも書かれていませんね。
点\((1,0)\)というのは、

このようにグラフから離れたところにある点なので接点ではありません。
ここを最初のパターンと混同しないように気を付けてください。
こういった場合には、まず接点を文字で置いてあげることからスタートします。
接点の\(x\)座標を\(a\)とすると、\(y\)座標は\(f(a)=a^2+3\)。
よって、接点は\((a,a^2+3)\)となります。
次に接線の傾きを求めましょう。
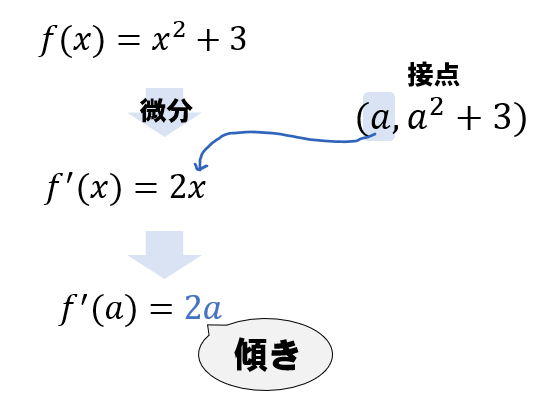
すると、接線の傾きが\(2a\)と表せました。
よって、傾き\(2a\)で接点\((a,a^2+3)\)ということから
接線の方程式は次のように表せます。
$$\begin{eqnarray}y-(a^2+3)&=&2a(x-a)\\[5pt]y&=&2ax-2a^2+a^2+3\\[5pt]y&=&2ax-a^2+3 \end{eqnarray}$$
ここまできたら、あと少し!
問題文から、この接線は点\((1,0)\)を通ると与えられているので
\(y=2ax-a^2+3\)に、\(x=1,\) \(y=0\)を代入して、\(a\)の値を求めましょう。
$$\begin{eqnarray}0&=&2a-a^2+3\\[5pt]a^2-2a-3&=&0\\[5pt](a-3)(a+1)&=&0\\[5pt]a&=&-1,3 \end{eqnarray}$$
\(a=3\)を接線の方程式 \(y=2ax-a^2+3\)に代入すると
$$y=6x-6\cdots(解)$$
\(a=-1\)を接線の方程式 \(y=2ax-a^2+3\)に代入すると
$$y=-2x+2\cdots(解)$$
イメージとしてはこんな感じです。
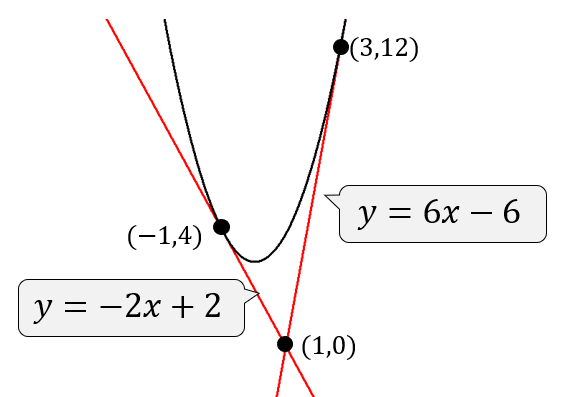
答え
$$y=6x-6$$
$$y=-2x+2$$
まとめ!
お疲れ様でした!
接線の式を求めるためには次の公式を覚えるという手もあります。
点\((a,f(a))\)における接線は
$$y-f(a)=f'(a)(x-a)$$
ですが、公式の見た目が難しそうですよね(^^;)
なので、今回の記事で紹介したように
手順で覚えておくのが良いかと思います。
接線の方程式は、テストや入試でも頻出の問題なので
たくさん練習して、確実に解けるようにしておきましょう!















まじでわかりやすかったです。
それなすぎる、、まじ助かった!