こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する式と証明の単元から「\((a+b+c)^3\)の展開」について取り上げます。
\((a+b)^3, (a-b)^3\) の公式は習ったけど、かっこの中が3つになってるやつは知らんけど…
と、困っている人が多いと思いますが心配はいりません^^
新しく公式を覚えたりすることなく計算することができますよ!(計算は大変だけど…)
それでは解き方をチェックしていきましょう!
サクッと理解したい方は、こちらの動画も参考にしてください!
メルマガ講座の中でYouTube講義のまとめサイトをお渡ししています。まとめサイトには動画講義のほか、定期テスト対策の特訓課題なども収録しているのでぜひご活用ください。無料で登録できるのでこちらからお願いします^^
\((a+b+c)^3\)の展開はかたまりをつくって考えるのがポイント!

こんな計算方法しらんけど…と思うかもしれませんが

このように、\(a+b\)をひとかたまりと考えて、\(a+b\)と\(c\)の2つをこれまで学習してきた3乗の公式に当てはめればOKです。
あとはそれぞれを展開しながらまとめていきましょう。(ここの計算が大変ですね><)
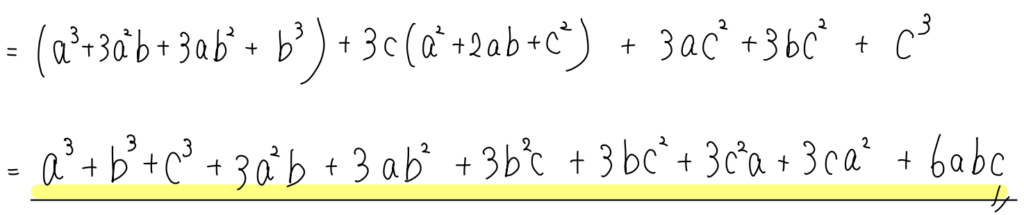
3乗の項を前に、次に\(ab → bc → ca \)の順になるように並べかえていますが、順番が違っていたとしてもそれぞれの項が出せていればOKです!
というわけで、かっこの中に3つあったとしても、やることはこれまでの3乗公式を使うだけですね。テストで出てきても戸惑うことなくサクッと解いちゃってくださいね^^
メルマガ講座でお渡ししているまとめサイトの中には、

このような3乗の基礎~発展までいろんな計算をイチから解説しています。これらもテストに出やすいですから合わせて学習しておきましょう!
メルマガ講座の無料登録はこちらから















コメントを残す