【整数の性質】15！は2で何回割り切れるか？

\(2\) で何回割り切れるかを求めるためには、

割られる数の中に因数 \(2\) が何個含まれているかを考えればよいです。

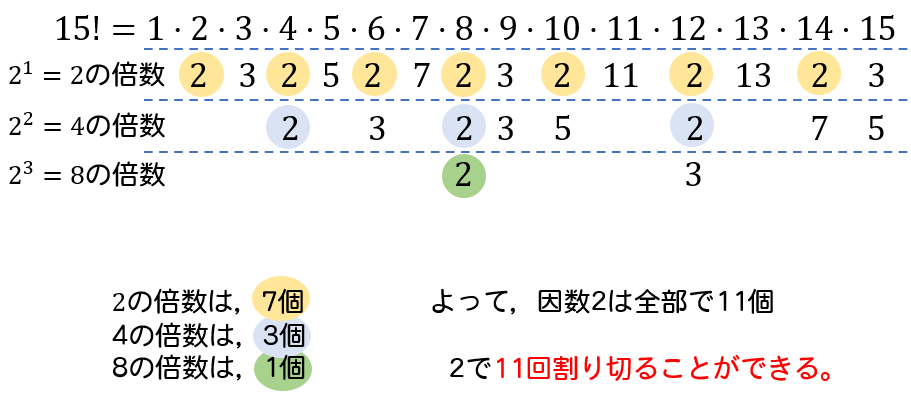
1から15までの数をそれぞれ素因数分解したとき、

1回目に因数2が出てくる数は、2を1つ以上含んでる数だから \(2\) の倍数です。

1から15までに2の倍数は、7個。

2回目に因数2が出てくる数は、1回目と合わせて2を2つ以上含んでいるわけだから\(2^2=4\) の倍数です。

1から15までに4の倍数は、3個。

3回目に因数2が出てくる数は、1，2回目と合わせて2を3つ以上含んでいる数だから\(2^3=8\) の倍数です。

1から15までに8の倍数は、1個。

4回目に因数2が出てくる数は、1，2，3回目と合わせて2を4つ以上含んでいる数だから\(2^4=16\) の倍数です。

ただ、1から15までに16の倍数はありませんので、

これ以上は因数2を含まないってことですね。

以上より、

因数2は合計で11個なので、2で11回割り切れるってことが求まります。

このように、それぞれの数を素因数分解したときの

1回目に出てくる2の数は、2の倍数

2回目に出てくる2の数は、4の倍数…というように数えていくことができます。

では、こちらの練習問題でサクッと理解を深めておきましょう。

では、最後にちょっとだけ応用問題も紹介しておきます！

\(10\) で何回割り切れるかを求めるためには、\(10=2\cdot 5\) より

割られる数の中に因数 \(2, \ 5\) が何個含まれているかを考えればよいです。

例えば、因数2が10個、因数5が6個含まれているなら

2と5を組み合わせて、因数10を6個作れるってことが分かります。

ただ、因数2と5の数を実際に数えてみれば分かるのですが、

因数5の数の方が少なくなります。

よって、因数5の個数がそのまま、因数10の個数と一致します。

というわけで、

因数5の個数を数えていきましょう。

1から55までに5の倍数は11個。

1から55までに25の倍数は2個。

よって、1から55までに含まれる因数5の数は13個となります。

したがって、因数10も13個なので、10で13回割り切れる。