高校数学Ⅰで学習する三角比の単元から
「3タイプの四角形についての面積」についてイチから解説していきます!
具体的には次の3タイプです。
【ノーマル四角形】
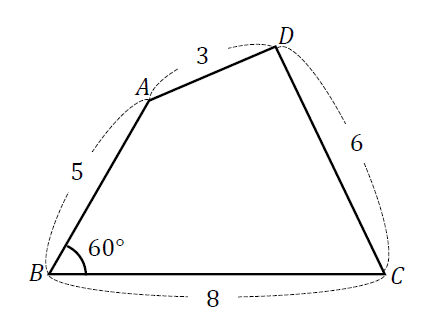
【円に内接する四角形】
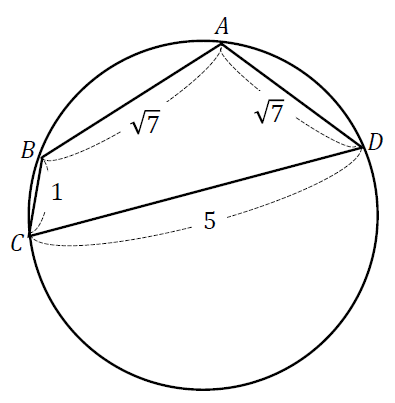
【対角線の長さがわかる四角形】
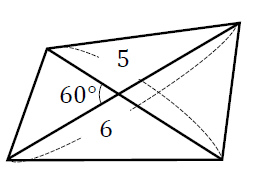
では、それぞれのタイプについて解き方、考え方を解説していきますね!
ノーマル四角形の面積
【問題】次の四角形の面積を求めなさい。

こちらの動画でサクッと解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
三角比の公式の中に、四角形の面積を一発で求めるものはありませんよね。
なので、次のように対角線を引いて2つの三角形に分割して考えていきましょう。
(対角線は、分かっている角度を残すように引いてください)
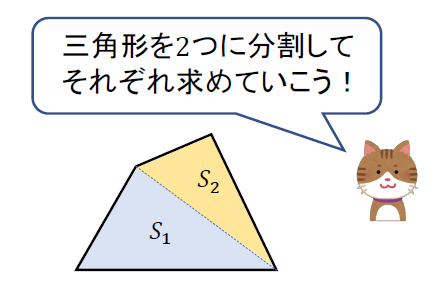
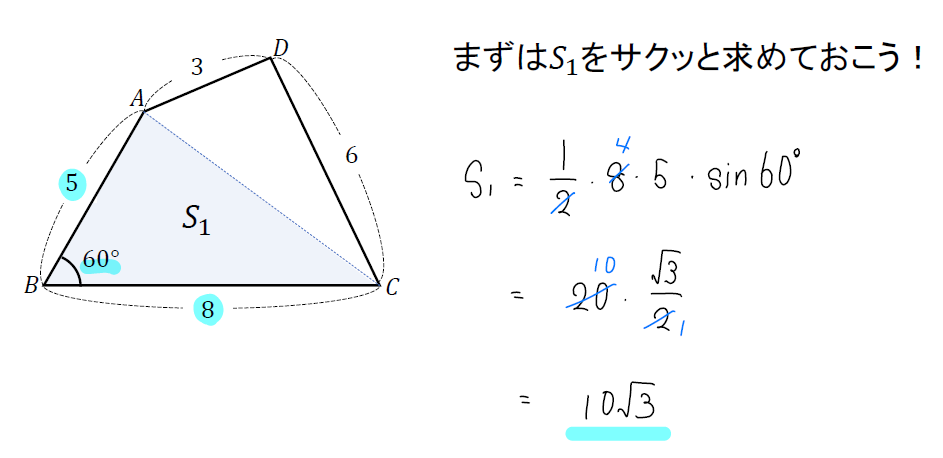
そして、角度が分かっている方の三角形の面積をサクッと求めておきましょう。
【三角形の面積を求める公式】
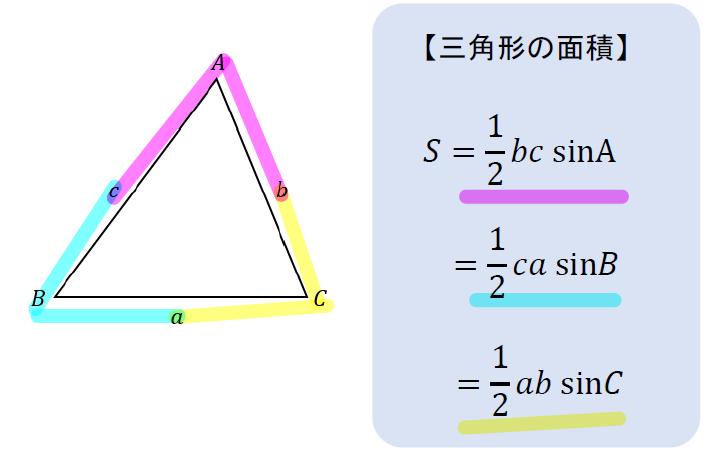
次に角度がわかっていないもう1つの三角形の面積を求めるのですが、これがメンドイ!
次の3STEPで求めていきます。
「対角線の長さ求める ⇒ sinの値を求める ⇒ 面積の公式に当てはめる」

ここでは余弦定理や三角形の相互関係などをフル活用します。
公式があいまいな方は、こちらの記事をご参考ください。
そして、2つの三角形の面積がそれぞれ求まったら
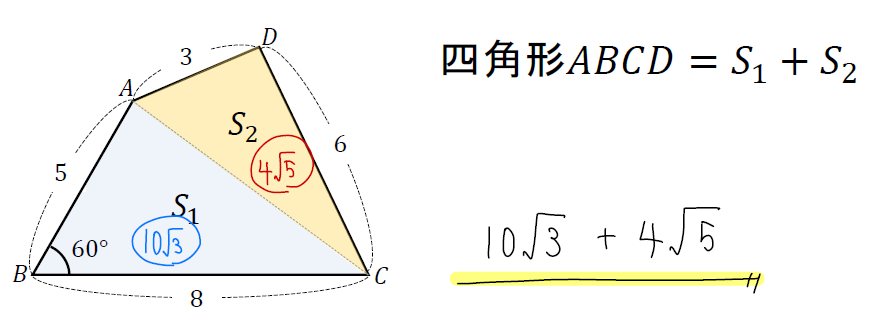
このように合計すれば四角形の面積の完成!というわけですね^^
演習チャレンジ!
では、理解を深めるためにこちらの問題にもチャレンジしてみましょう!
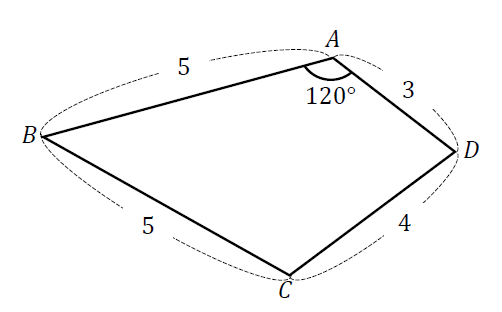
【問題】次の四角形の面積を求めなさい。
1番出る!円に内接する四角形の面積
【問題】次の四角形の面積を求めなさい。

こちらの動画でサクッと解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
円に内接する四角形は頻出!
絶対におさえておきたい問題です。
この問題では、まず最初におさえておきたいポイントがあります。
それがこちら!
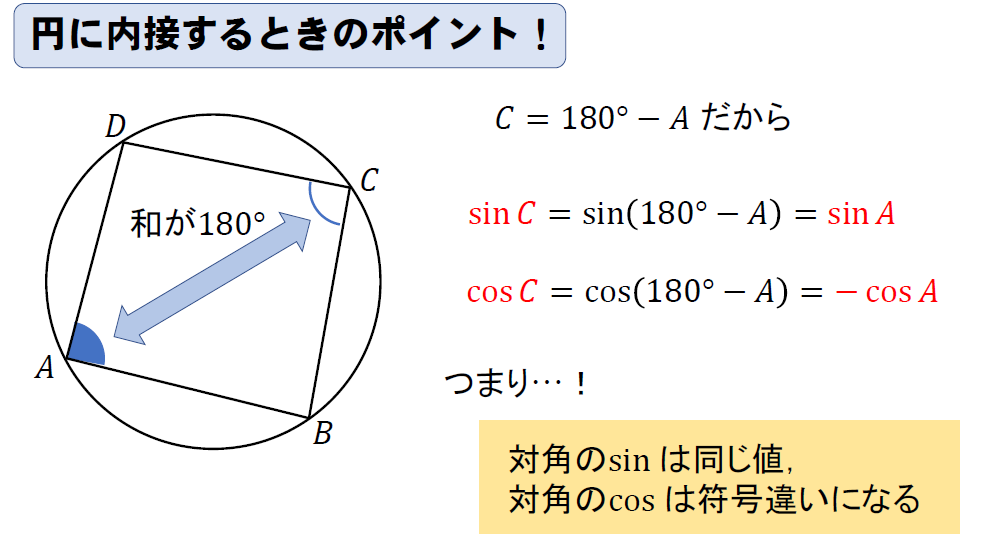
円に内接する四角形は対角の和が180°になります。
そのため、対角にあるsinはまったく同じ値に、cosは符号違いになるという特徴があります。
これをおさえておかないと次に進めないので、まずは頭に叩き込んでおいてください。
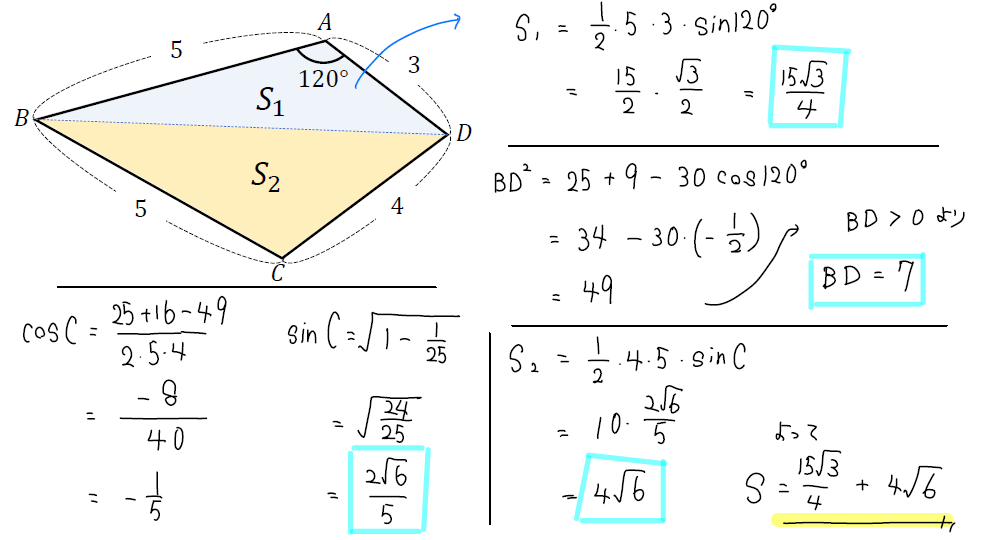
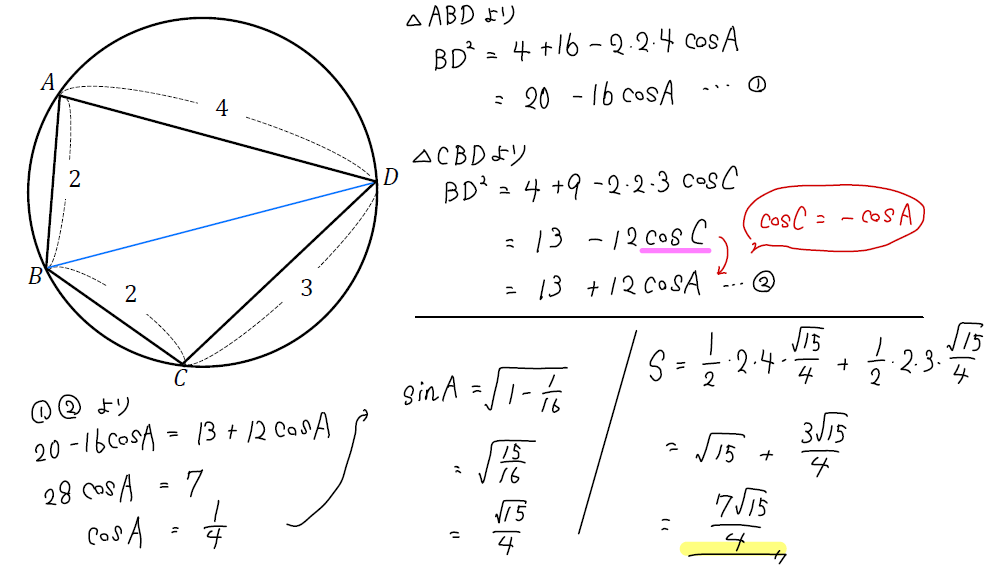
まずは対角線をひいて2つの三角形にわけます。(ノーマルタイプと同じ流れ)
そこから余弦定理、相互関係を使いながら下のように
「対角線の2乗の式をつくる ⇒ 方程式をつくってsinを求める」という2STEPで計算を進めていきます。
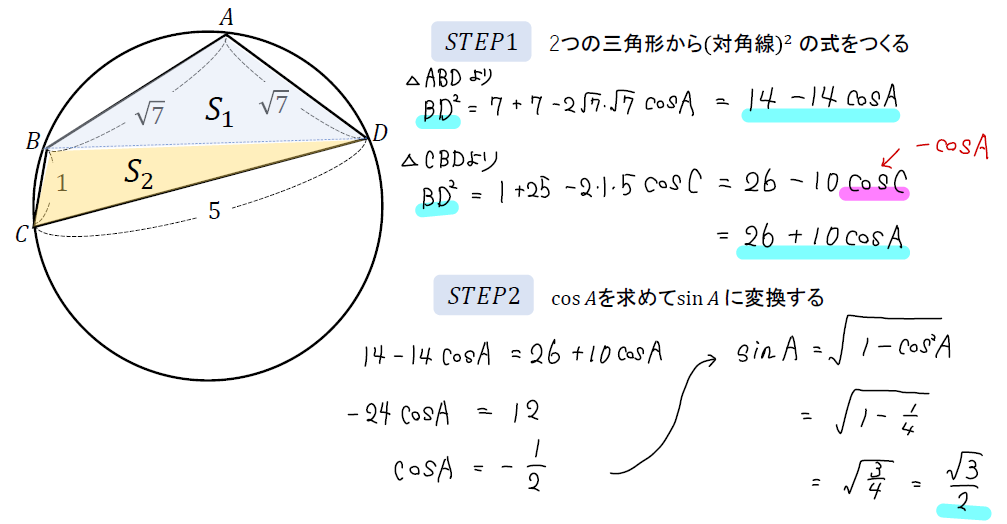
ここでは円に内接する四角形の対角の性質を利用して「\(\cos{C}=-\cos{A}\)」と変換しているのがポイントです。
対角にあるsinは同じ値になることを利用して、それぞれの三角形の面積を求めます。
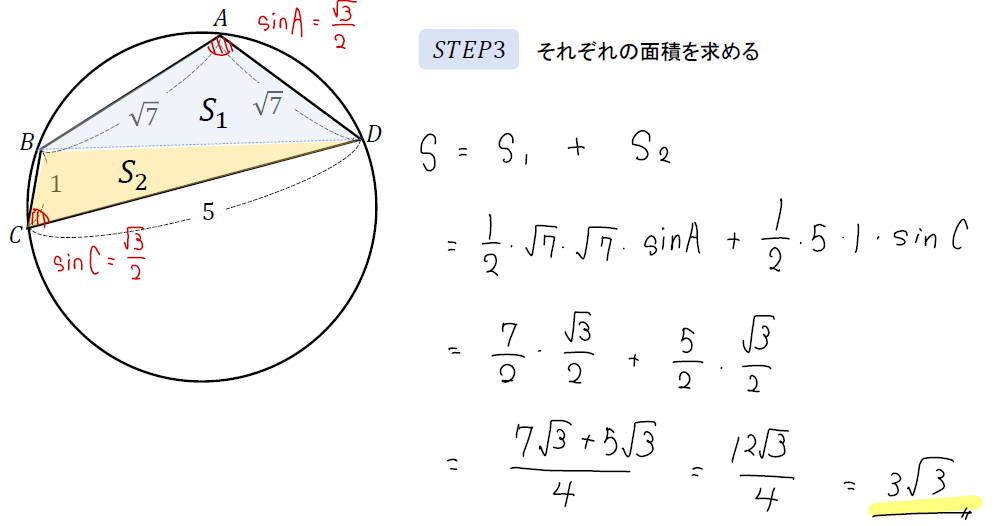
これで四角形の面積の完成です!
最初に説明したポイントをおさえておけば簡単に計算を進めていくことができますね^^
では、演習にチャレンジしましょ(‘ω’)ノ
演習にチャレンジ!
【問題】次の四角形の面積を求めなさい。
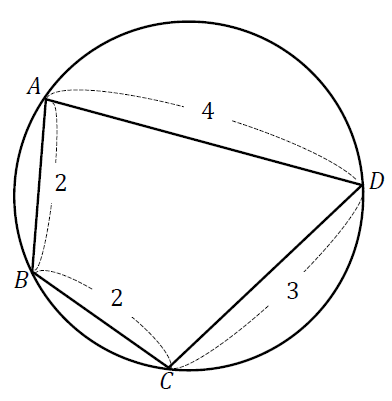
対角線の長さから四角形の面積
【問題】次の四角形の面積を求めなさい。

こちらの動画でサクッと解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
四角形の対角線とそのなす角度が与えられたときは超ラッキー!!
なぜなら…次の公式を使うだけで1分で解けちゃうからです(/・ω・)/
【対角線と四角形の面積公式】
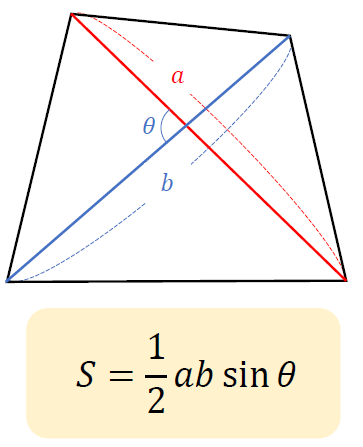
これにあてはめて計算すると
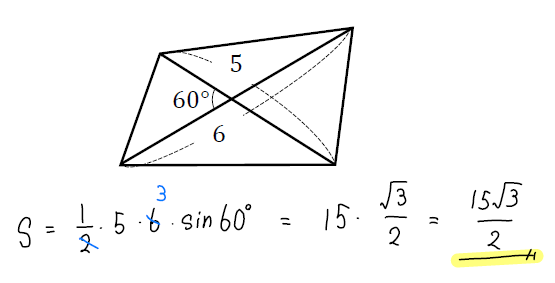
たったコレだけの計算で解けちゃいます!
使いどころの少ない公式ですが、便利なので覚えておくといいですよ^^
公式の証明
この公式について証明させる問題が出てくることがあります。
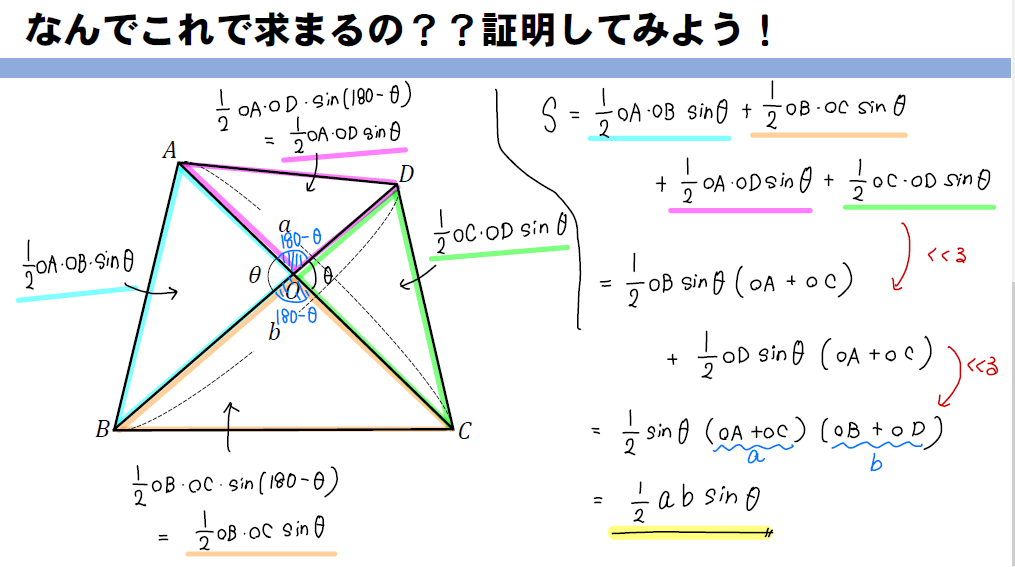
計算過程はちょっと複雑ですが、このように4つの三角形に分割して、くくり出しを利用しながらまとめていくと公式の証明が完成します。
上の画像だけではゴチャっとしてて分かりづらいと思うので、動画解説も参考にしてみてね!
まとめ
というわけで、今回は3タイプの四角形の面積について解説しました。
中でも円に内接する四角形はよく出てくるので、スラスラと解けるように練習してくださいね!
三角比の他記事はこちらのページでまとめているので、どんどん学習を進めていきましょう(‘ω’)ノ
















コメントを残す