三角比を含む等式の証明のやり方をイチから！

こんにちは！数スタの小田です。

今回は高校数学Ⅰで学習する三角比の単元から「等式の証明」について取り上げます。

 

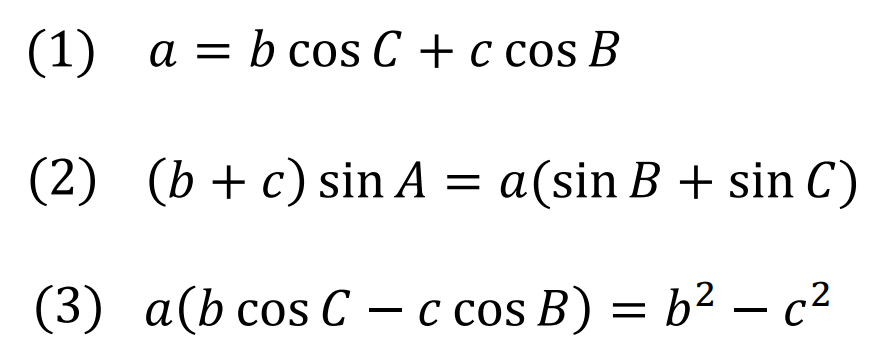
「等式の見た目が難しそう…」「証明ってどうやるの…」

と、戸惑ってしまうかもしれませんが、安心してください＾＾

この問題はやり方がわかってしまうと、フツーの計算問題じゃん！って感じでスラスラ解けるようになりますよ！

 

サクッと理解したい方は、こちらの動画も参考にしてください！

等式の証明手順

等式に含まれる\(\sin , \cos\)を変形して、左辺＝右辺になることを確かめましょう！

それぞれの変形には、\(\sin\)なら正弦定理、\(\cos\)なら余弦定理を使います。

 

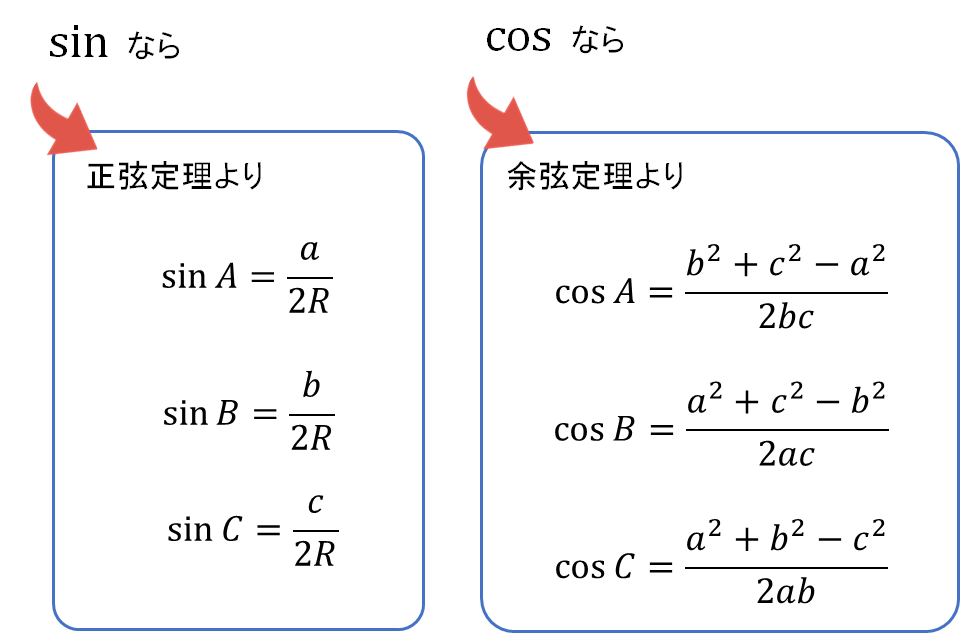
これらの定理を覚えていない方は、こちらの記事も参考にしてくださいね！

三角比の等式証明

それでは具体的に証明のやり方を確認していきましょう。

（1）の解説

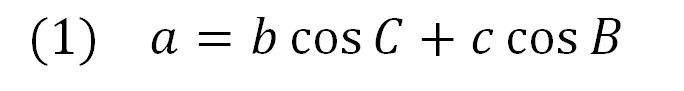
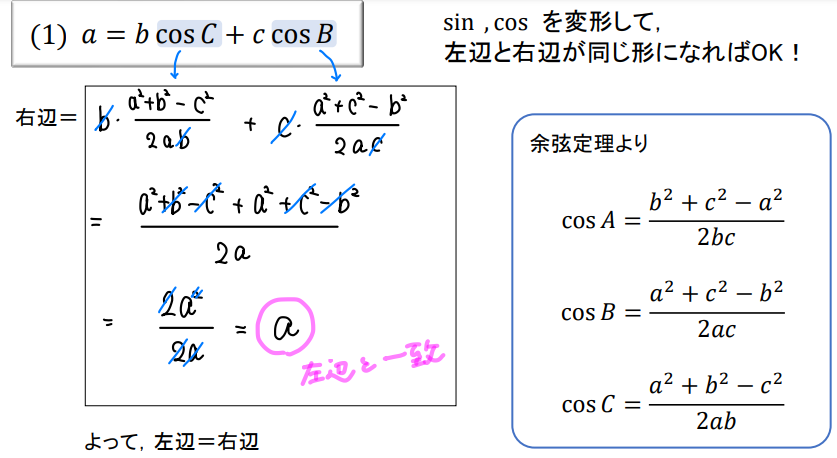
まず、等式の中で\(\sin, \cos\)を含む辺を取り出します。

この等式であれば左辺には\(\sin, \cos\)が含まれていないのでそのまま置いといて、右辺だけを取り出しましょう。

そして、右辺の\(\cos\)を余弦定理を用いて変形していきます。

計算をがんばって進めていくと、\(a\)となり左辺と見た目が同じになりましたね！

よって、左辺と右辺が等しくなることが確かめられたので証明完了となります。

 

証明と言っても、やってることはただの計算問題と一緒ですよね＾＾

（2）の解説

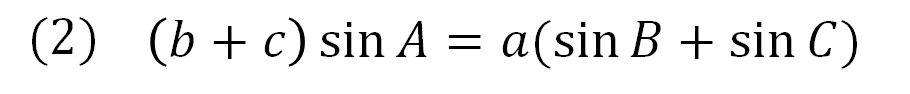
今回は左辺、右辺ともに\(\sin\)が含まれているので、両方の辺を取り出します。

まずは左辺を取り出し、正弦定理を用いて変形すると、\(\frac{a(b+c)}{2R}\)というちょっとゴツいのがでてきました。なんじゃこりゃって思うかもしれませんが、このまま置いておきます。

次に右辺を取り出し、同じように正弦定理で変形しましょう。すると、右辺の方も同じく\(\frac{a(b+c)}{2R}\)になります。

 

よって、左辺と右辺を変形したところ同じ見た目になったので、左辺と右辺は等しい！証明完了だ！！となるわけです。

（3）の解説

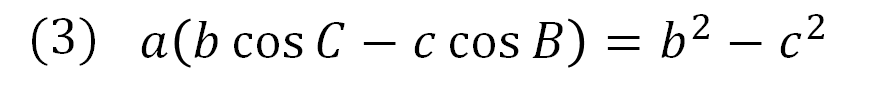
（3）も、これまでと同じ流れでやっていけばOKです！

\(\cos\)が含まれている左辺を取り出して、余弦定理で変形していきましょう。

計算はちょっとメンドイですが…細かく約分をしながらまとめてください。すると、\(b^2-c^2\)となり右辺と同じになることが確かめられますね！ってことで証明完了(‘ω’)ノ

 

 

というわけで、今回は三角比を含む等式の証明について解説しました！

証明とはいえ、やってることは正弦定理、余弦定理を使って計算してるだけですよね＾＾

あまり難しく考えずにサクッと解けるようになってもらえると嬉しいです！

 

今回の問題ができるようになると、次は「三角形の形状決定」というちょっと発展的な問題も理解できるウようになります。よかったら続けてこちらもチャレンジしてみてくださいね！

⇒　【三角比】どんな三角形になる？形状決定のコツをイチから解説！