【数学Ⅰ】三角比を含む不等式の解き方、考え方を解説！

高校数学Ⅰで学習する三角比の単元から

「三角比を含む不等式の解き方」

について解説していきます。

 

取り上げる問題はこちら！

 

これらの不等式を解くためには、三角比を含む方程式について理解しておく必要があります。

方程式どうやるんだっけ…？

と、不安がある方は上の記事で確認しておいてくださいね！

 

今回の内容はこちらの動画でも解説しています！

三角比 \(\sin\) を含む不等式

\(\sin\) は \(y\) として考えていきます。

そのため、（1）のように \(\cdots>\frac{1}{2}\) というのは、

\(y\) 座標が \(\frac{1}{2}\) よりも大きく（上）なっている範囲を求めよ。という意味になります。

単位円をかいて、\(y\) 座標が \(\frac{1}{2}\) よりも上の部分に色をつけて角の範囲を求めると次のようになります。

 

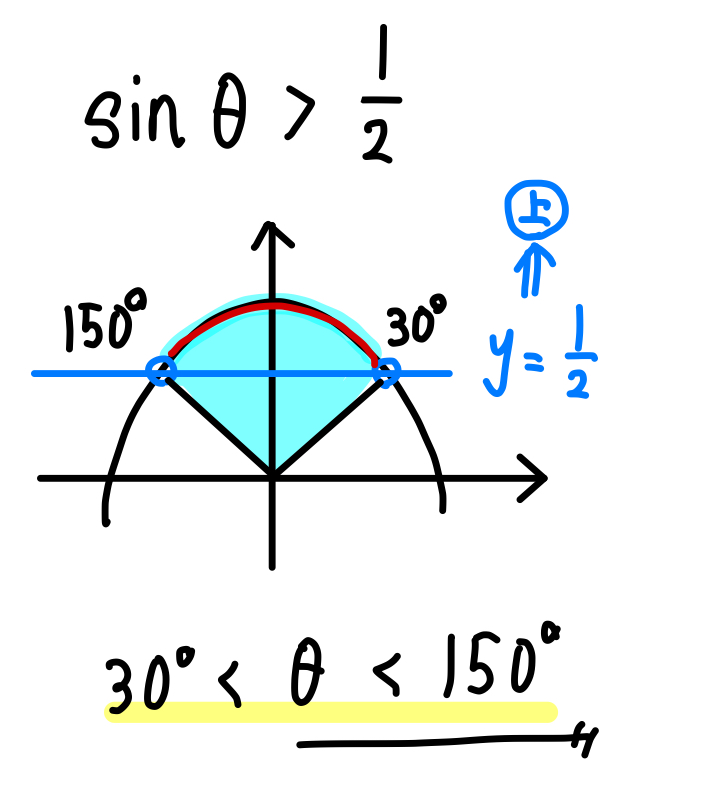
一方で（2）のように、\(\cdots≦\frac{\sqrt{3}}{2}\) というのは、

\(y\) 座標が \(\frac{\sqrt{3}}{2}\) 以下（下）になっている範囲を求めよ。という意味になります。

よって、単位円をかいて色をつけていくと次のような範囲になります。

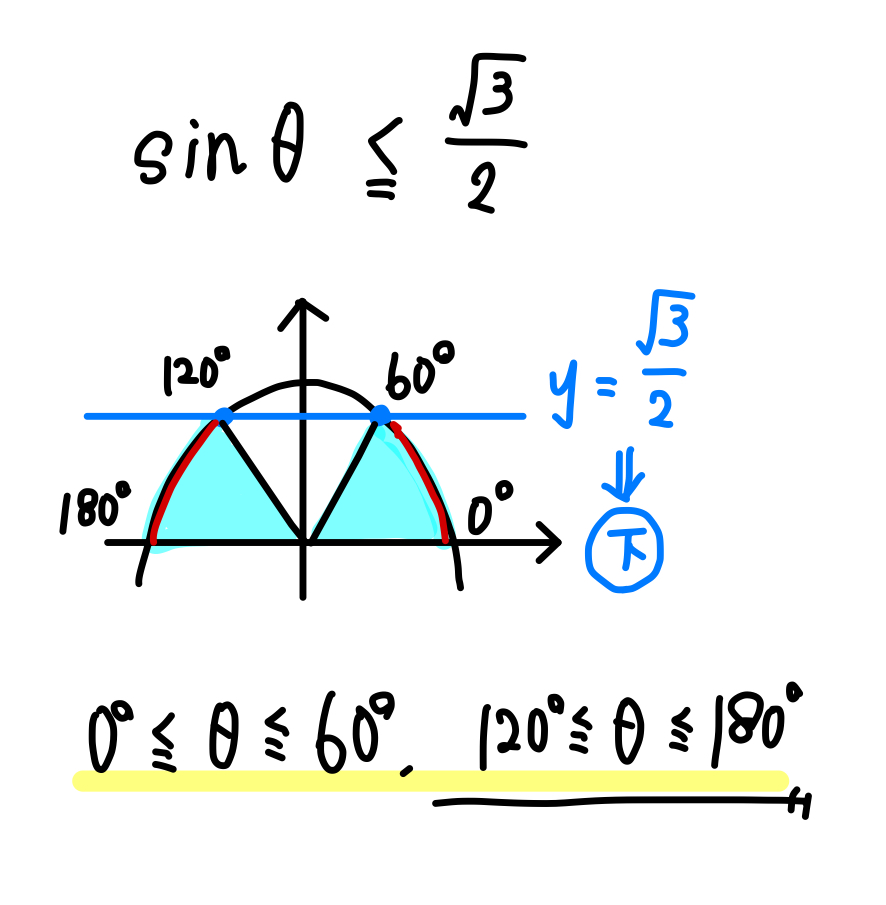
以下になっている部分は、右側と左側の2つに分かれてるってのもポイントですね。

三角比 \(\cos\) を含む不等式

\(\cos\) は \(x\) として考えていきます。

そのため、（3）のように \(\cdots<-\frac{1}{\sqrt{2}}\) というのは、

\(x\) 座標が \(-\frac{1}{\sqrt{2}}\) よりも小さく（左）なっている範囲を求めよ。という意味になります。

単位円をかいて、\(x\) 座標が \(-\frac{1}{\sqrt{2}}\) よりも左の部分に色をつけて角の範囲を求めると次のようになります。

 

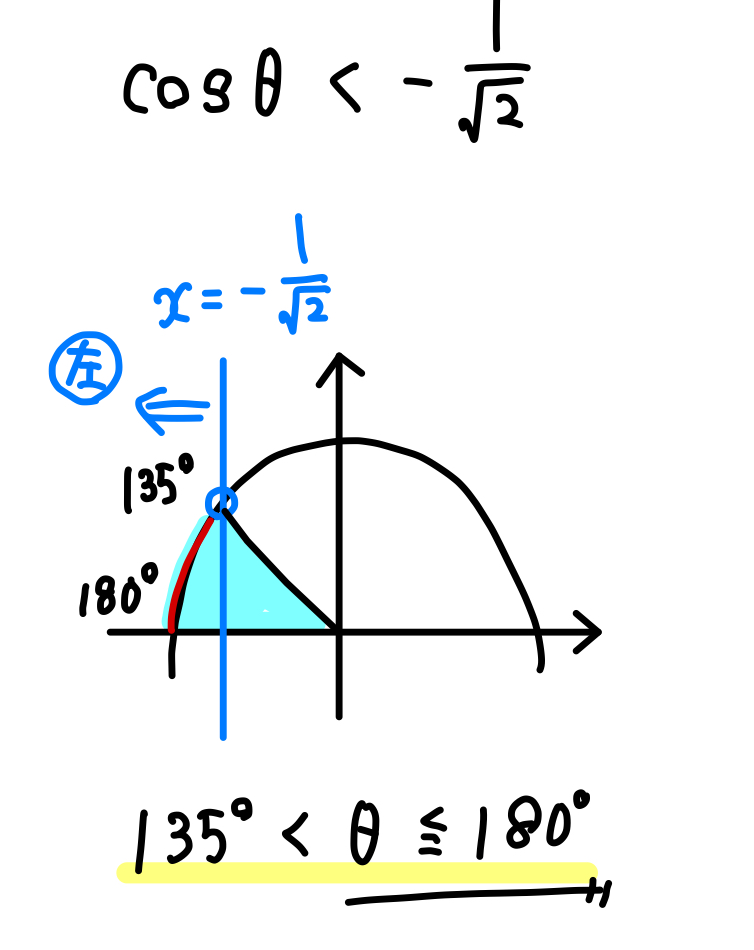
一方で、（4）のように \(\cdots ≧\frac{1}{2}\) というのは、

\(x\) 座標が \(\frac{1}{2}\) 以上（右）になっている範囲を求めよってことですね。

 

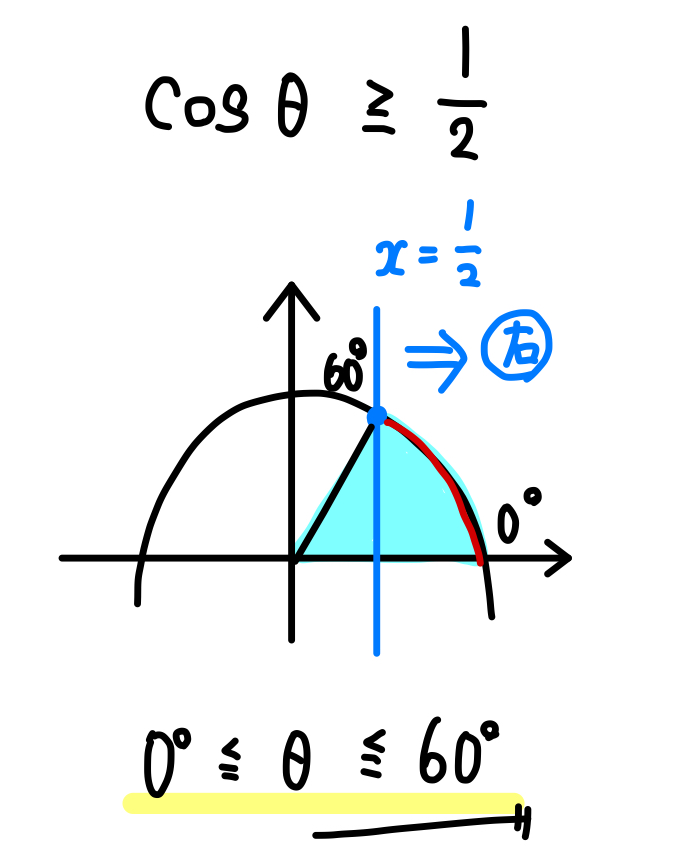
三角比 \(\tan\) を含む不等式

\(\tan\) は 傾き として考えていきます。

\(\tan\) はちょっとイメージしづらいかもしれませんね(^^;)

だけど、慣れてくれば大丈夫！

こちらの解説をよく見といてくださいね。

 

まず、（4）のように \(\cdots ≧\sqrt{3}\) というのは、傾きが \(\sqrt{3}\) 以上になる範囲を求めろってことです。

では、具体的にどの部分を表しているかというと、

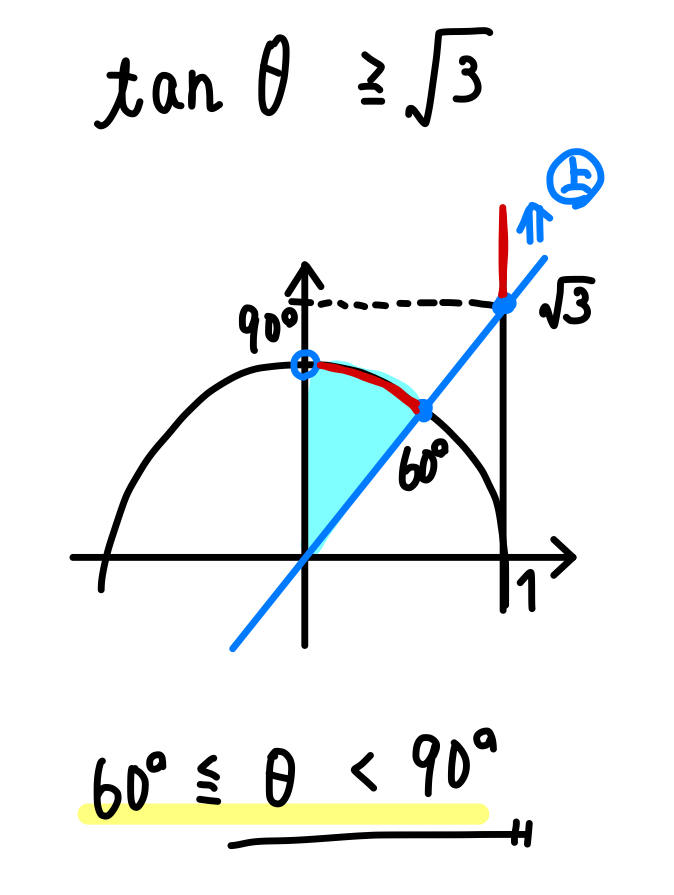
このような範囲になります。

\((1,\sqrt{3})\) より上の部分で交わる直線はすべて傾きが \(\sqrt{3}\) 以上になります。

そのような直線が引ける範囲を求めると上のような範囲になるというわけです。

 

気を付けておきたいポイントとしては…

\(\tan\) を考える場合、90°の角は含まれない！

という点ですね。\(\tan90°\) の値は存在しないんだったよね。

だから、範囲を考える場合には90°を含まないように気を付けてください。

 

最後に、（6）のように \(\cdots<1\) の場合。

つまり、傾きが \(1\) よりも小さくなる範囲を求めると、

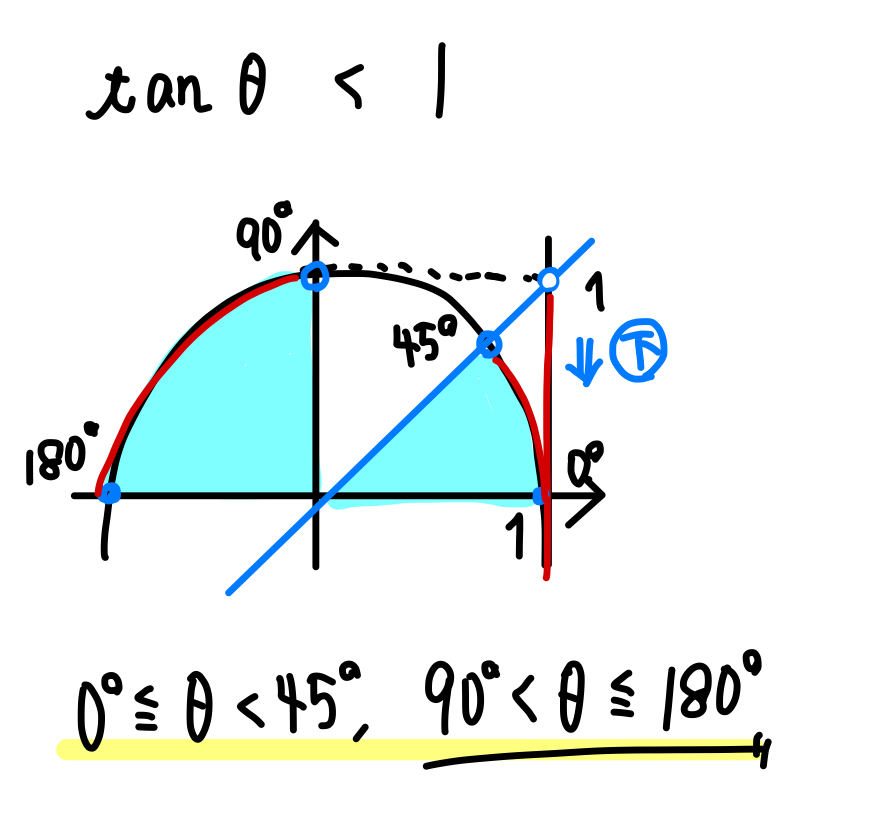
このような範囲になります。

\((1,1)\) より下の部分で交わる直線はすべて傾きが \(1\) より小さくなります。

 

なんで第2象限の90°から180°の範囲も含まれるの？

と、疑問を感じるかもしれませんね。

私も学生時代に、悩んでいた経験があります…(^^;)

 

しかし、理由は単純です。

第2象限の範囲では、直線の傾きは常に負になります。

なので、どの部分を通っていても常に \(<1\) を満たしてるってことになるよね。

 

まとめ！

お疲れ様でした！

三角比を含む不等式は理解できましたか？

この問題は後に数学Ⅱで学習する「三角関数」の単元において、めちゃくちゃ重要になってきます。

なので、今のうちにしっかりと理解しておいてくださいね。

 

ポイントとしては、不等号の向きから

単位円上のどの部分を見ていけばいいのかを理解しておくことです。

以上の点をしっかりと覚えておきましょう(^^)