今回は中学3年生で学習する
『円周角の定理』から
角度を求める問題を徹底的に解説していくよ!
今回解説していく問題はこちら





これは分かるぜ!っていう問題は目次ページから飛ばして読んでいってくださいな。
では、いくぞー!
円周角の定理についてはこちらの動画でも解説しています(‘◇’)ゞ
円周角の定理とは
まず、問題を解いていく上で知っておいて欲しい知識がこちら

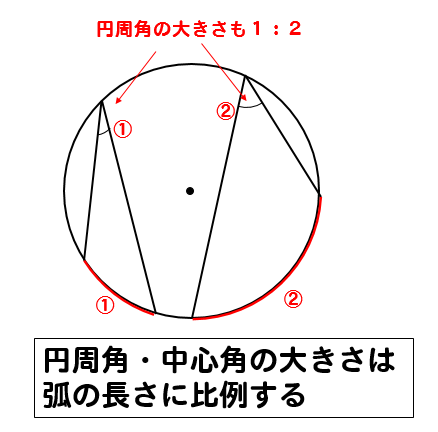
- 同じ弧に対する中心角の大きさは円周角の大きさの2倍


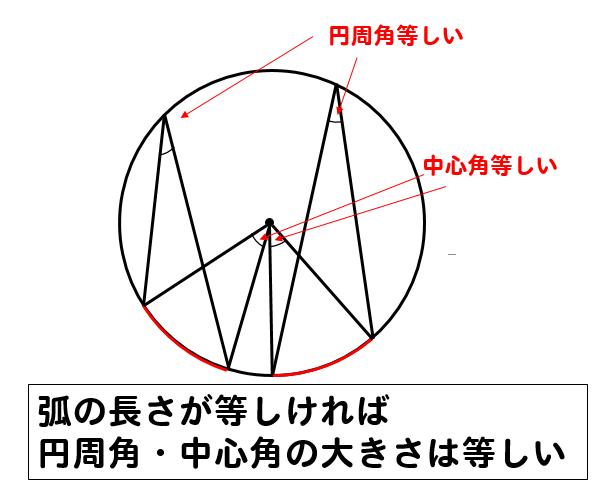
- 弧の長さが等しければ、円周角・中心角の大きさは等しい

同じ弧でなくても長さが等しければ、円周角、中心角は等しくなります。


それでは、以上のことを頭に入れておいて
問題に挑戦してみましょう!
(1)(2)円周角の定理 基本問題解説!
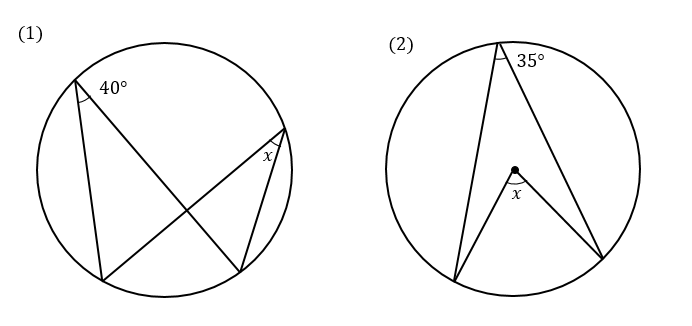
次の∠xの大きさを求めなさい。

(1)解説&答えはこちら
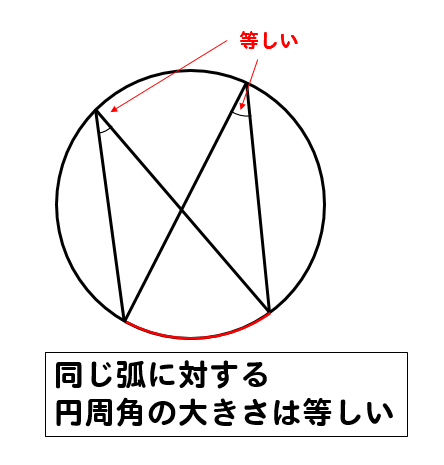
同じ弧に対する円周角の大きさは等しくなるので

\(x\)も40°となります。
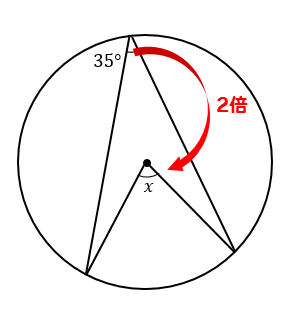
(2)解説&答えはこちら
(2)の問題では、中心角と円周角の関係より

中心角である\(x\)は円周角35°の2倍となります。
これらは楽勝問題ですね!
円周角の定理をしっかりと覚えておけば大丈夫なはずです。
では、少しずつ難易度を上げていきましょう。
(3)(4)見た目がややこしい 問題解説!
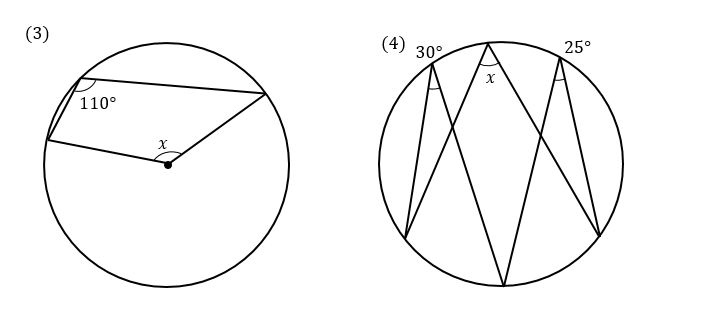
次の∠xの大きさを求めなさい。

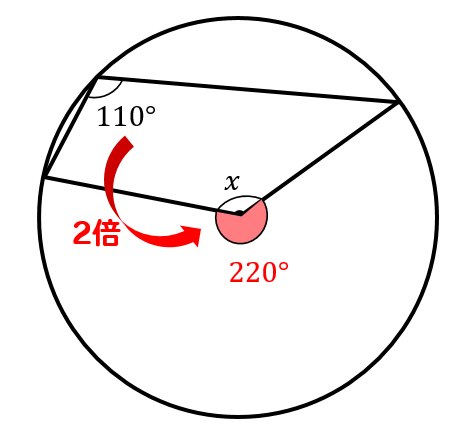
(3)解説&答えはこちら
簡単そうに見えるのですが、引っかかって間違える人が多い問題です。
110°の角に対する中心角の位置を間違えないでください。

中心角は220°となるので
$$∠x=360-220=140°$$
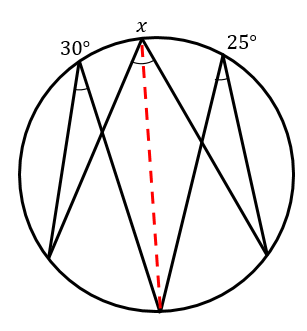
(4)解説&答えはこちら
この問題…なんかすごいですね
とげとげしいです。

こういった、とげとげ円周角の場合
補助線を書いて考えていきます。

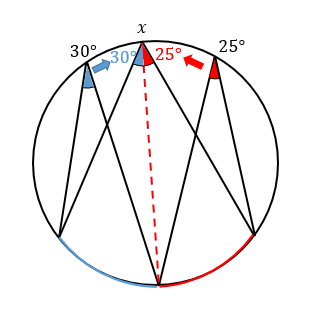
すると、30°と50°の円周角をみると

∠xの大きさは30°と25°を合わせた角だと分かります。
$$∠x=30+25=55°$$
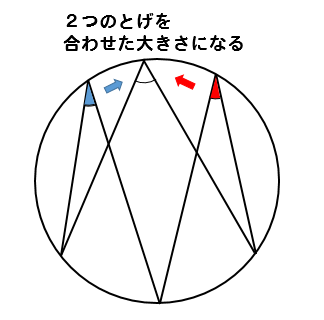
とげとげ円周角は
2つのとげを合わせると、真ん中のとげになる!

(5)(6)直径に対する円周角、弧の長さ等しい問題解説!
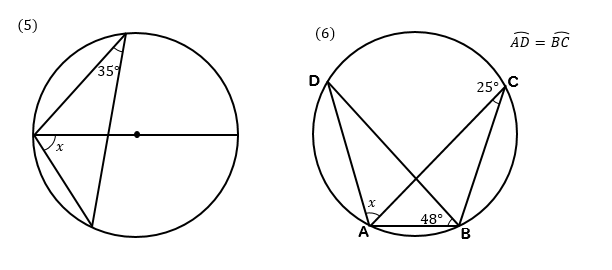
次の∠xの大きさを求めなさい。

(5)解説&答えはこちら
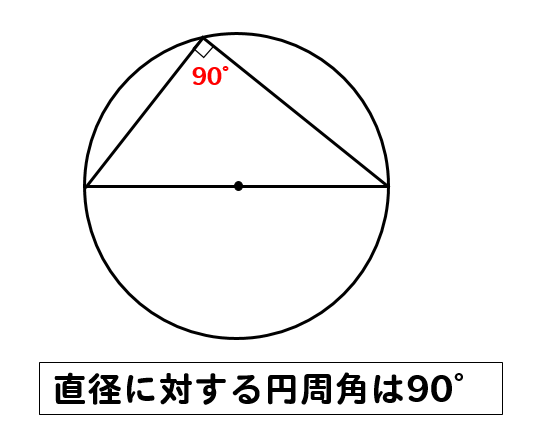
直径を表す線がある場合には

この性質を使って、90°の角を見つけます。

そこから角をたどっていくと

$$∠x=55°$$
となります。
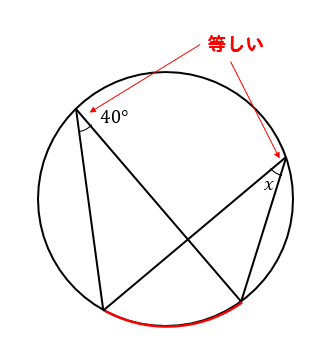
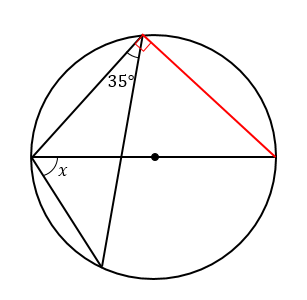
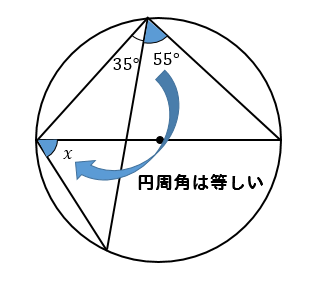
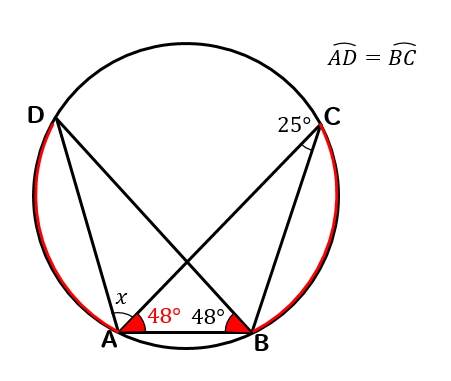
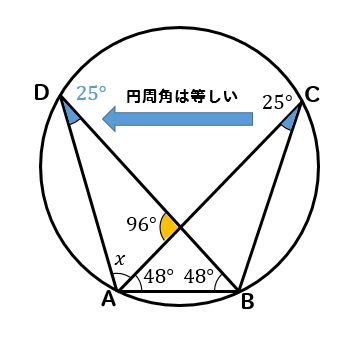
(6)解説&答えはこちら
\(\stackrel{ \Large \frown }{ AD }=\stackrel{ \Large \frown }{ BC }\)より
長さが等しい弧に対する円周角の大きさは等しくなるので

\(∠CAB=48°\)ということがわかります。
ここからいろいろと角をたどっていくと

$$∠x=180-25-96=59°$$
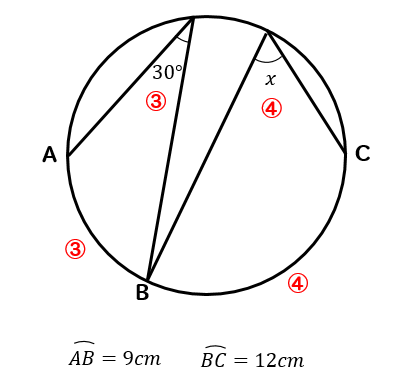
(7)(8)弧の長さと比に関する円周角の問題解説!
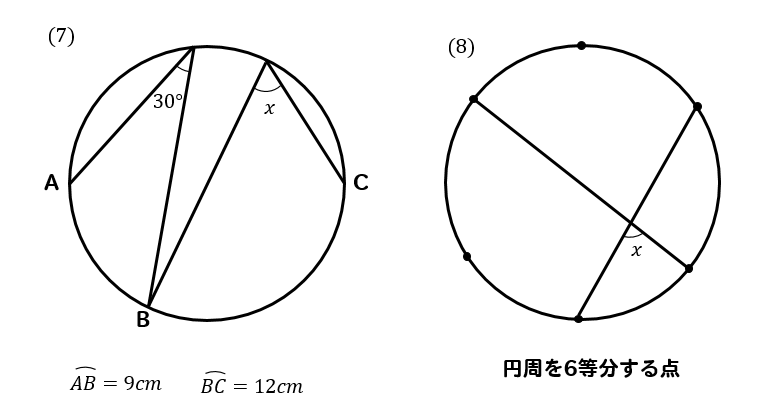
次の∠xの大きさを求めなさい。

(7)解説&答えはこちら
弧の長さの比が円周角の大きさの比になるので

$$3:4=30:x$$
$$3x=120$$
$$x=40$$
(8)解説&答えはこちら
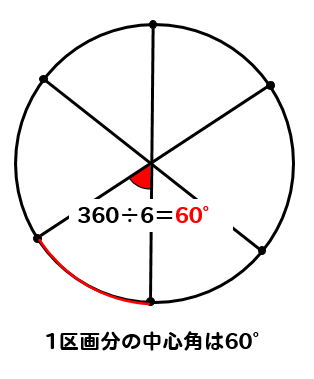
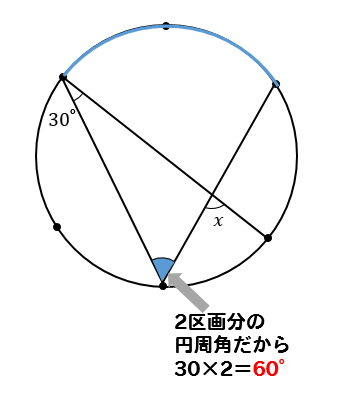
このように○等分というような問題は
1区画分の中心角、円周角を求めることが大事です。
6等分の場合

1区画分の中心角の大きさは
\(360\div 6=60°\)となります。
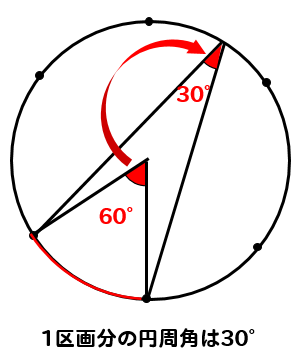
そして、その1区画分の円周角は
中心角の半分の大きさになるので

1区画分の円周角の大きさは30°となります。
6等分の場合
1区画分の中心角は60°、円周角は30°
これを利用しながら問題を考えていきます。
補助線を1本引いて、1区画分の円周角の大きさを求めます。

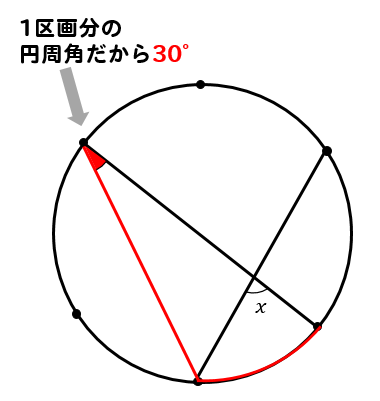
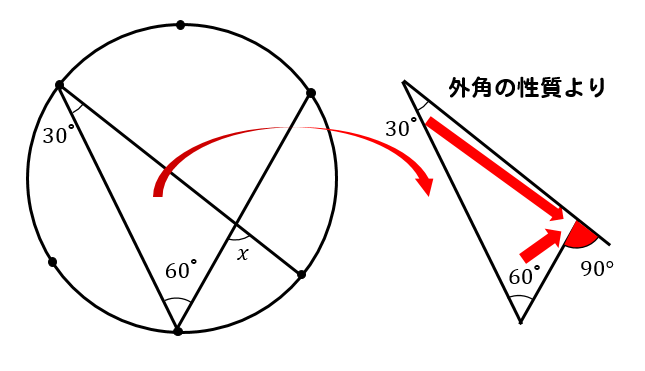
次は、2区画分の円周角に注目して、大きさを求めます。

1区画分の円周角が30°だから
2区画分の場合は30×2=60°となります。
最後に三角形の外角に注目すると∠xの大きさを求めることができます。

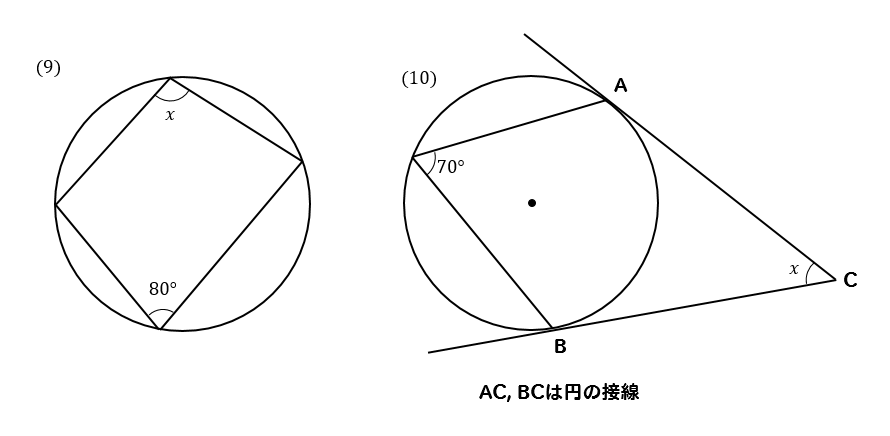
(9)(10)内接する四角形、接線に関する問題解説!
次の∠xの大きさを求めなさい。

(9)解説&答えはこちら
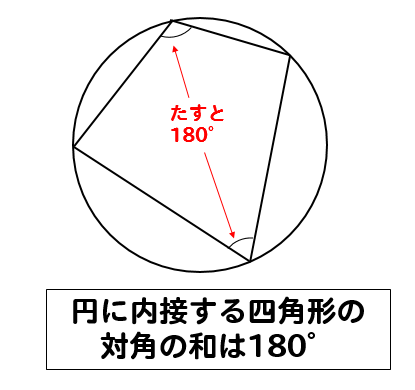
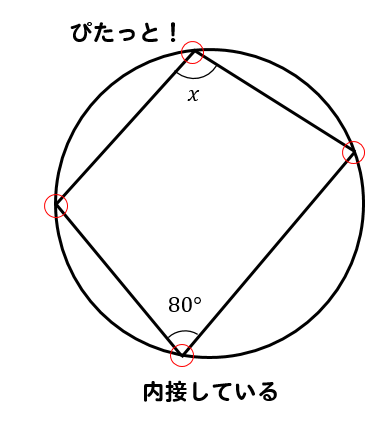
四角形が円に内接していますね。
内接っていうのは
円の中にぴたっとはまっている状態のことね!

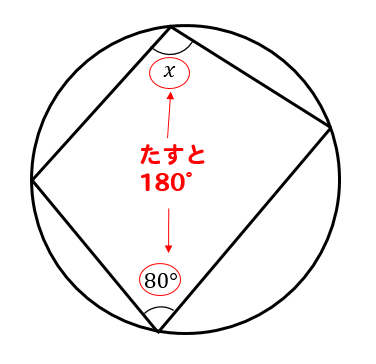
このように四角形が円に内接しているときには
四角形の対角の和が180°になるという特徴があります。

これを利用すると
$$∠x=180-80=100°$$
内接の性質を覚えておけば簡単ですね!
なんで対角の和は180°やねん!!
オレは納得いかねえぇぇぇ!

という方はこちらをご参考くださいませ。

(10)解説&答えはこちら
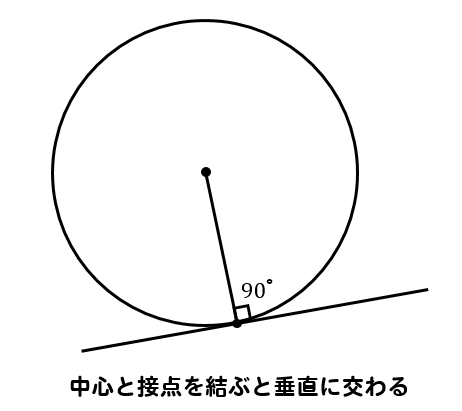
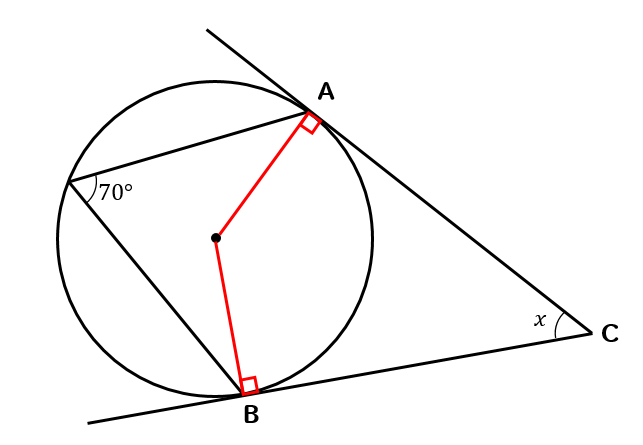
この問題では接線が出てきます。
接線が出てきたときには
中心と接点を結んで90°の角を作ってやりましょう!

中心と接点を結ぶと90°の角ができるという特徴があるので
補助線を引いて90°の角を作ります。

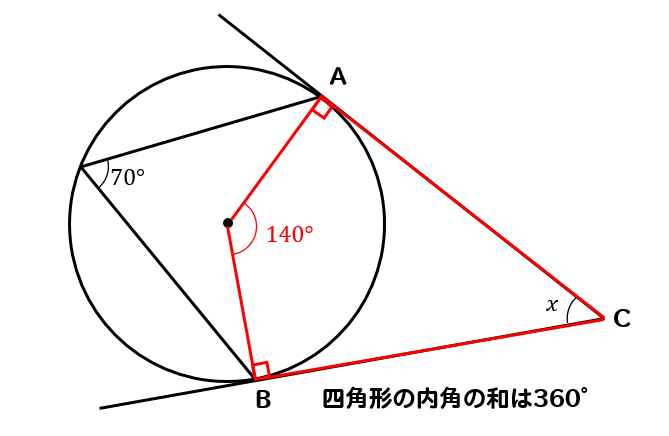
そこから中心角などをたどっていくと


四角形の内角の和は360°なので
$$∠x=360-(90+90+140)=40°$$
となります。
接線が出てきたら
補助線を引いて90°を作る!というのがポイントですね。
円周角の問題まとめ
問題演習お疲れ様でした。
円周角の問題を解いていくために大切な問題をパターン別に解説していきました。
今回解いてもらった問題を全て理解することができるれば
他の問題に関しても
ちょっと思考を変えるだけで解くことができるはずです。
まずは今回の10問を完璧にしておきましょう!
慣れてくるとパズルを解くような感覚で面白いですよ(^^)
さぁ、たっくさん問題演習して理解を深めていこう。
ファイトだー(/・ω・)/




















最初の5,6の問題が見えないのですが…
バグでしょうか?
訂正しておきました!!
あるがとう
お役に立ててよかったです!
勉強がんばってくださいね^^
分かりましたありがとうございます。
非常にわかりやすいです
頑張って次のテストに挑もうと思います
ありがとうございます^^
テスト応援してます(‘ω’)ノ
とてもわかりやすかったです
明日のテスト頑張ります!!
テストがんばってください!
ファイト、ファイト(/・ω・)/
テスト1時間前にこのサイトを見つけることができてよかったです!本当に助かりました。ありがとうございます!
テストが上手くいっているといいな^^
わかりやすい説明ありがとうございました。
次のテストにやる気が出てきました!!
よかったです^^
テストがんばってください!!
わかりやすかったです
嫌いな円周角が好きになれました。ありがとうございます