こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する図形と方程式の単元から「2つの円の共通接線の求め方」についてイチから解説していきます。
取り上げる問題はこちら!
【問題】次の2つの円の両方に接する直線の方程式をすべて求めなさい。
(1)\(x^2+y^2=4\), \((x-6)^2+y^2=16\)
(2)\(x^2+y^2=4\), \((x-4)^2+y^2=1\)
共通接線の求める手順はテキストによっていろいろなやり方が紹介されていますが、今回は僕が一番やりやすいと感じている「接点を文字で置く」という解き方でやっていきますね!
たぶんコレが一番シンプルだと思うので(‘ω’)ノ
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
2円の共通接線(1)の解説
【問題】次の2つの円の両方に接する直線の方程式をすべて求めなさい。
(1)\(x^2+y^2=4\), \((x-6)^2+y^2=16\)
まずは、2つの円の中心、半径をチェックして簡単な図をかいてみましょう!
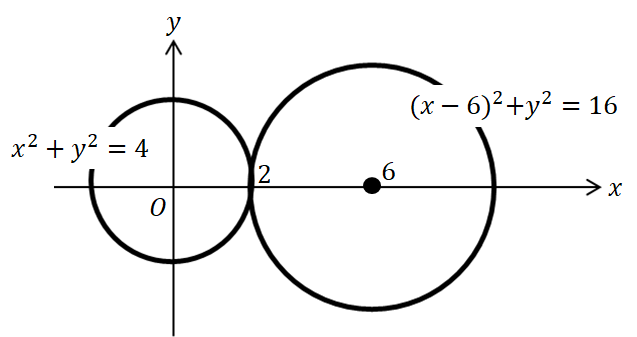
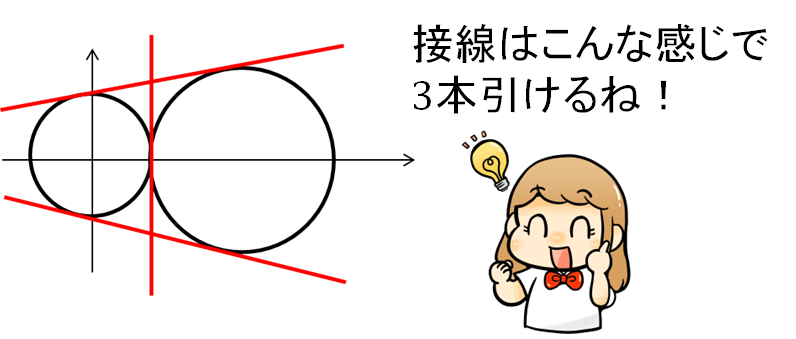
すると、こんなイメージ図がかけますね!
このことから今回の共通接線は3本あることがわかります。
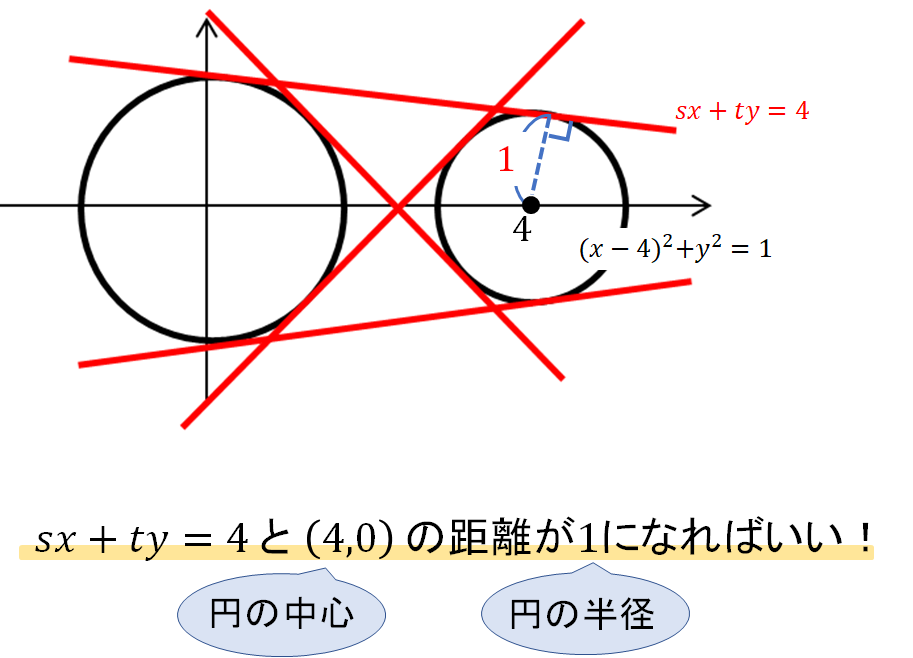
次に \(x^2+y^2=4\) 上にある接点を\((s,t)\) とおいて次の式をつくります。
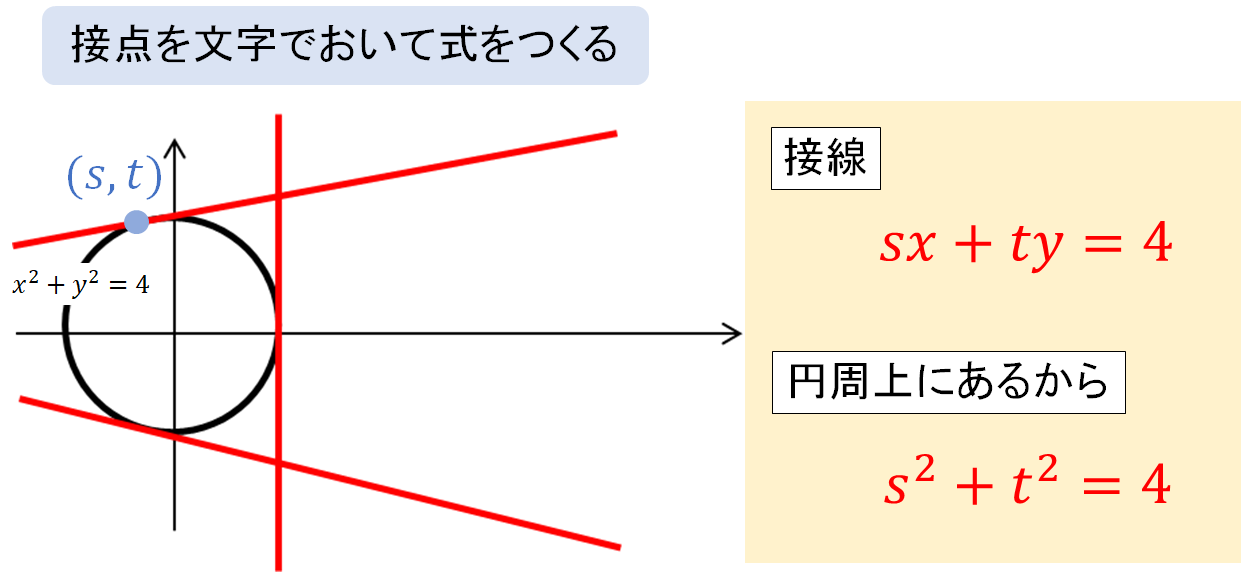
接点を文字でおくことで、仮の接線の式がつくれるだけでなく、接点は円周上にある点なので円の方程式に代入した式もつくることができます。これはあとから利用していくようになるので、この段階でつくっておいてください。
そして、2つの円に接するということは、今つくった接線が\((x-6)^2+y^2=16\) とも接する必要があります。接するためには次の条件を満たしていればOKです。
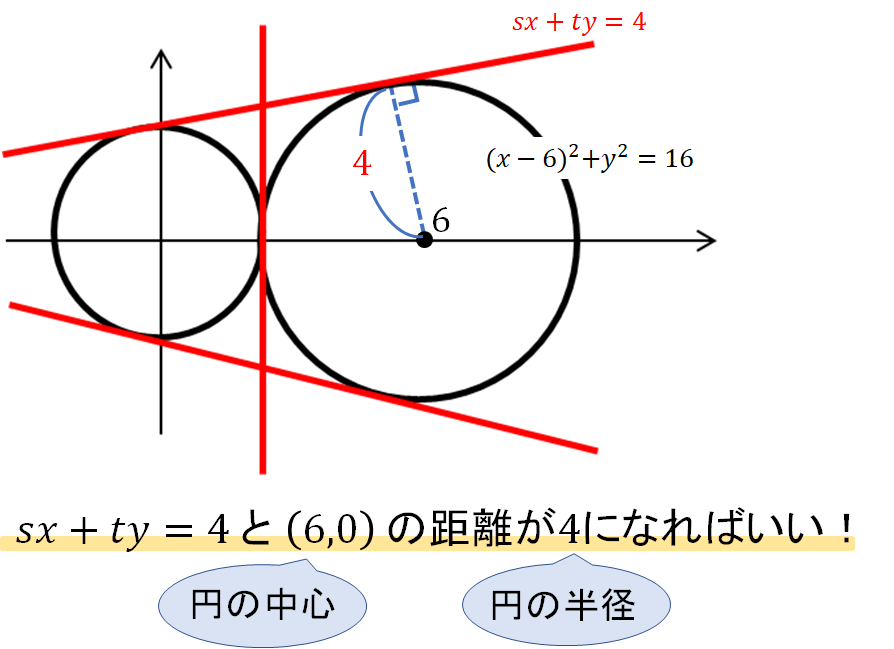
というわけで、直線と距離の公式を使って方程式をつくっていきましょう。
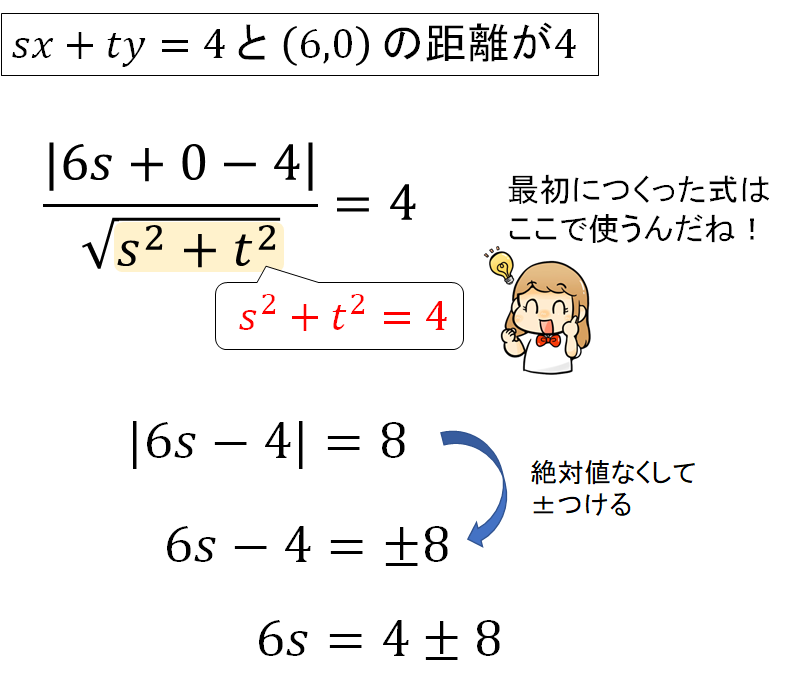
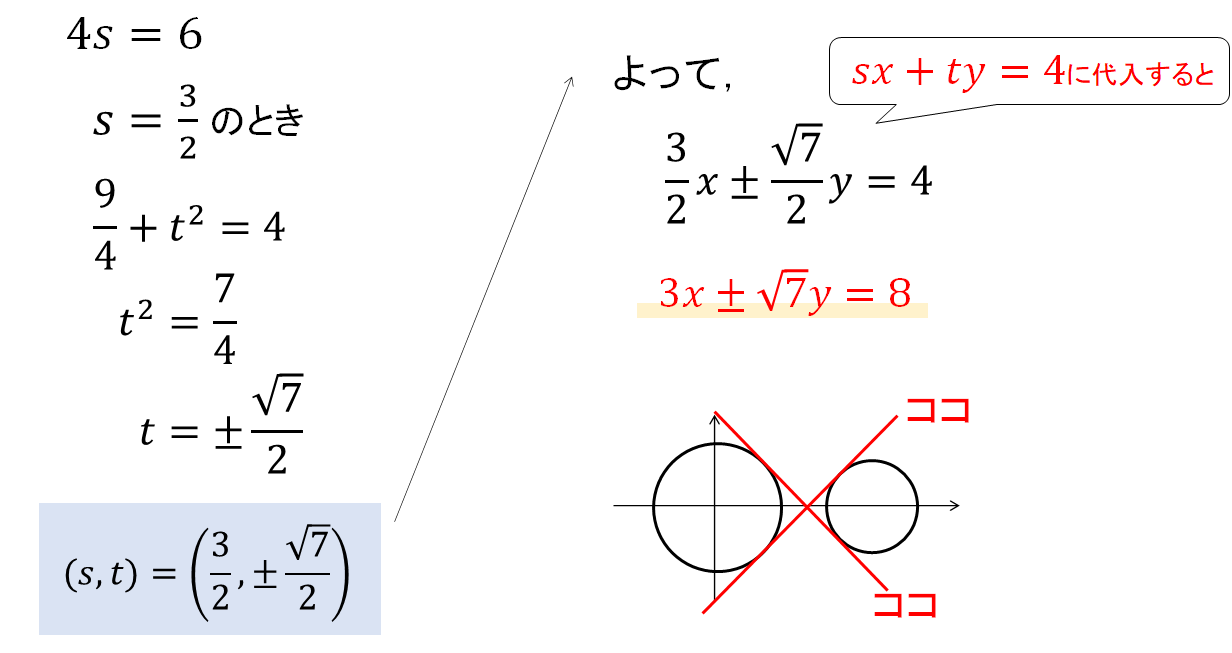
すると、sの値が2つ求まるので、それぞれの場合で計算を進めてください。
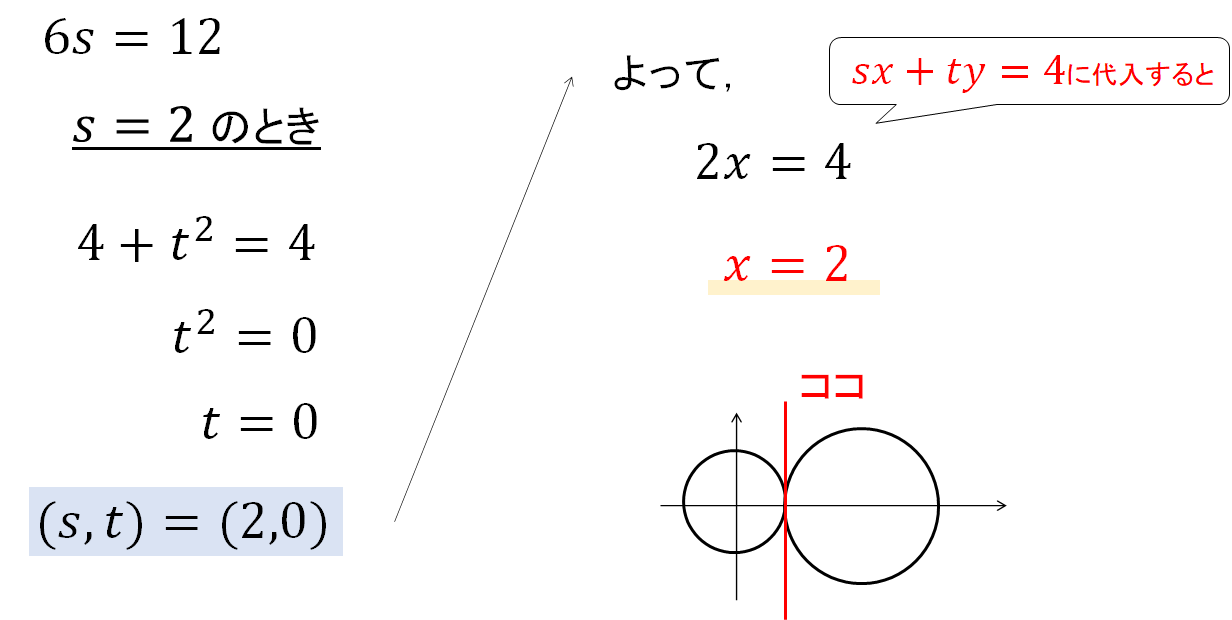
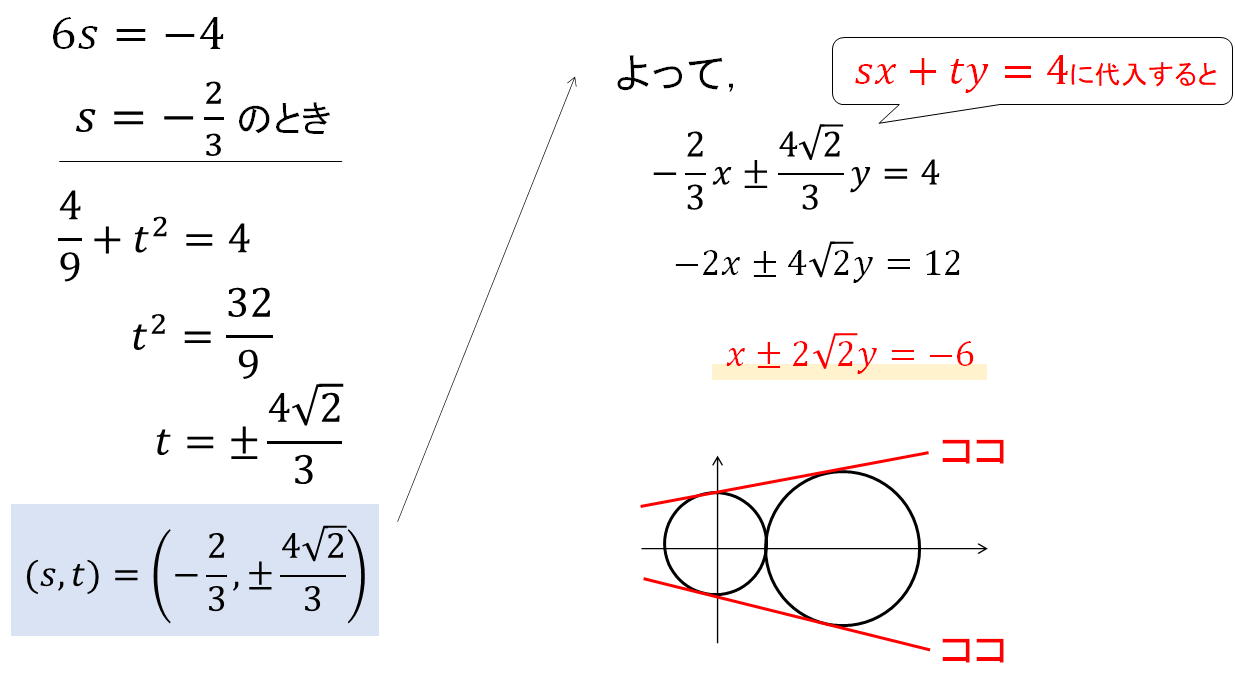
というわけで、接線の方程式が3本できあがりです!
途中の計算がちょっとややこしいところもあるので、冒頭で紹介した解説動画を参考にしてもらえると、より理解度がアップすると思います^^
答え
$$x=2$$
$$x\pm2\sqrt{2}y=-6$$
2円の共通接線(2)の解説
【問題】次の2つの円の両方に接する直線の方程式をすべて求めなさい。
(2)\(x^2+y^2=4\), \((x-4)^2+y^2=1\)
解いていく流れは(1)と全く同じ。サクッとやってみましょう!
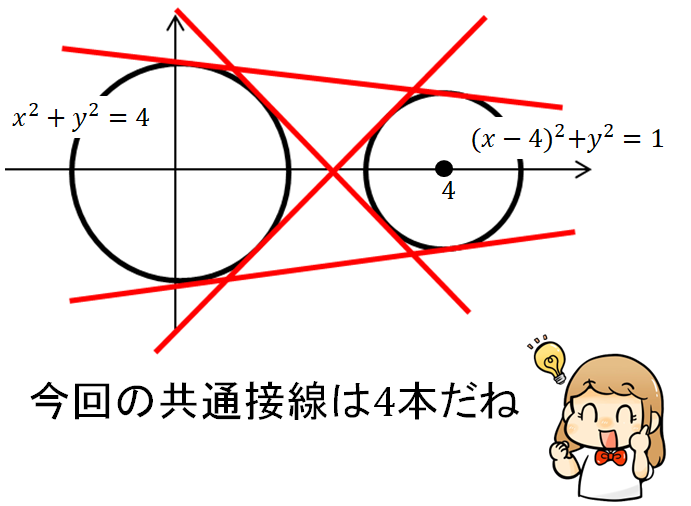

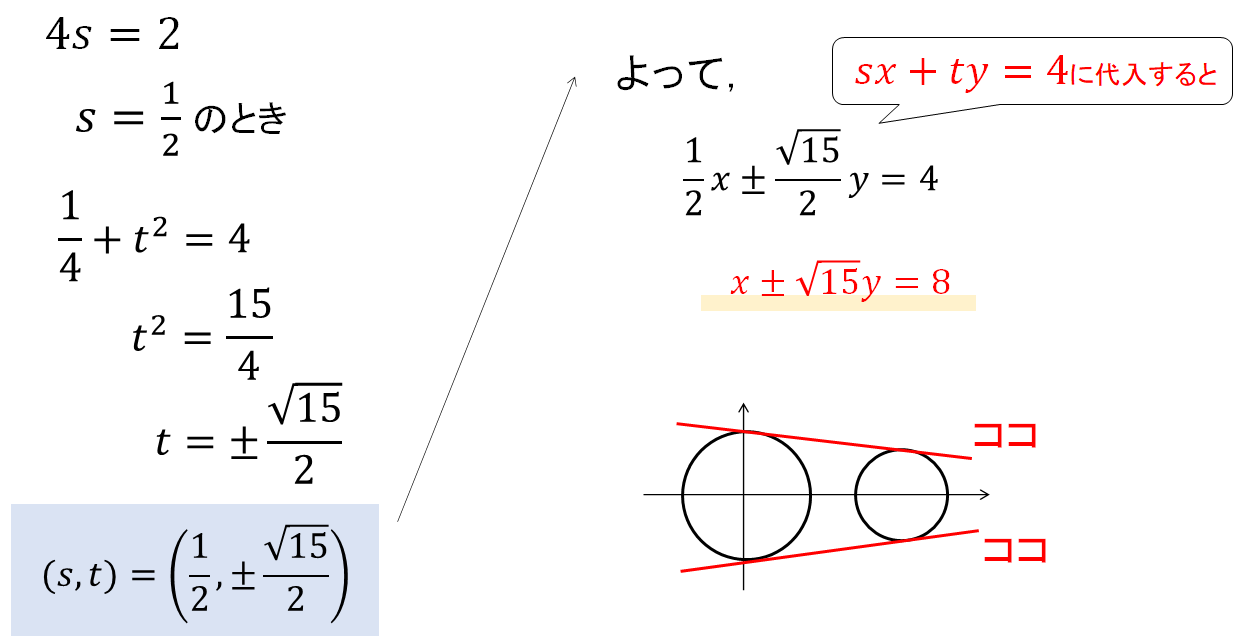
答え
$$3x\pm\sqrt{7}y=8$$
$$x\pm\sqrt{15}y=8$$
まとめ
お疲れ様でした!
今回の内容を文章だけでお伝えするのは結構ムズイ!!
なので、ちょっとでもわかりづらいところがあれば、動画講義の方も参考にしてもらえると助かります^^
ということで、動画講義をもう1度貼っておきますね(‘ω’)ノ

















わか「やすかったです!