【三角比の相互関係】公式３つの覚え方と使い方は？？

今回は、高校数学Ⅰで学習する三角比の単元から

「三角比の相互関係」

に関する問題を解説していきます。

三角比の相互関係とは

このような３つの関係式のことをいいます。

だけど、これがね…

覚えにくい！

とくに③の式は使う頻度も少ないだけに忘れてしまいがち(^^;)

というわけで、今回の記事では三角比の相互関係の式を自分で作る方法、相互関係の式を使った問題の解き方について説明していきます(^^)

今回の内容はこちらの動画でも解説しています！

【三角比の相互関係】公式３つの覚え方と使い方は？？

では、それぞれの式の作り方について解説していきます。

\(x, y, r\) 、3つの文字を使って説明していきます。

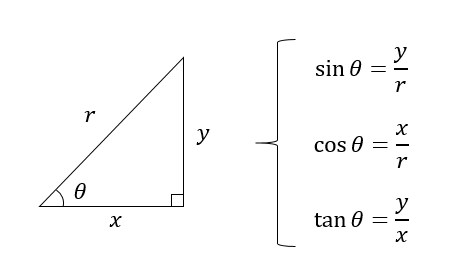
①\(\sin^2\theta+\cos^2\theta=1\)

上に示したように、三角比より

$$\sin\theta=\frac{y}{r},  \cos\theta=\frac{x}{r}$$

と表すことができます。

これらの式を変形すると

$$\begin{eqnarray} \sin\theta&=&\frac{y}{r}\\\sin\theta\times r&=&\frac{y}{r}\times r\\r\sin\theta&=&y\end{eqnarray}$$

$$\begin{eqnarray} \cos\theta&=&\frac{x}{r}\\\cos\theta\times r&=&\frac{x}{r}\times r\\r\cos\theta&=&x\end{eqnarray}$$

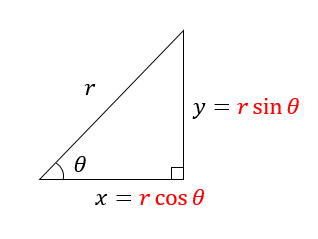
このように考えることができますね。

そして、直角三角形では三平方の定理が成り立つので

$$\begin{eqnarray} (r\sin\theta)^2+(r\cos\theta)^2&=&r^2\\[5pt]r^2\sin^2\theta+r^2\cos^2\theta&=&r^2\\[5pt]両辺をr^2で割ると\\[5pt]\color{red}{\sin^2\theta+\cos^2\theta=1}\end{eqnarray}$$

このように式を作ることができますね(^^)

sinの2乗とcosの2乗を足したら1になる！

覚えておきましょう。

②\(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\)

次は、\(\displaystyle{\tan\theta=\frac{y}{x}}\) に\(x=r\cos\theta\)、\(y=r\sin\theta\)を代入することで導くことができます。

$$\begin{eqnarray}\tan\theta&=&\frac{y}{x}\\[5pt]&=&\frac{r\sin\theta}{r\cos\theta}\\[5pt]&=&\frac{\sin\theta}{\cos\theta} \end{eqnarray}$$

よって、\(\color{red}{\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}}\)

となります。

③\(\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}\)

これが一番覚えにくいよねｗ

だけど、大丈夫！相互関係の①②を覚えておけば簡単に導くことができます。

\(\sin^2\theta+\cos^2\theta=1\) の両辺を\(\cos^2\theta\) で割ればよいです！

$$\begin{eqnarray}(\sin^2\theta+\cos^2\theta)\div \cos^2\theta&=&1\div \cos^2\theta\\[5pt]\frac{\sin^2\theta}{\cos^2\theta}+1&=&\frac{1}{\cos^2\theta}\\[5pt]\left(\frac{\sin\theta}{\cos\theta}\right)^2+1&=&\frac{1}{\cos^2\theta}\\[5pt]\tan^2\theta+1&=&\frac{1}{\cos^2\theta}\end{eqnarray}$$

このように、①の式を\(\cos^2\theta\)で割り、②の式を代入することで導くことができます。

これで、試験中に忘れてしまっても大丈夫ですね(^^)

【三角比の相互関係】問題の解き方は？？

それでは、三角比の相互関係を使った問題の解き方についてみていきましょう。

基本問題①

まず、注目すべきは\(\theta\) の大きさです。

問題文より、\(\cos\) の値が負になるということから、\(\theta\) は鈍角になるということが分かります。

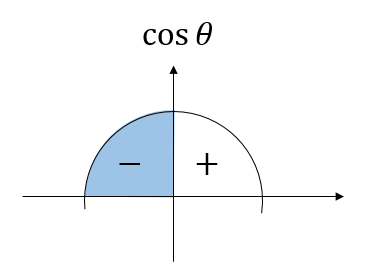
よって、\(\sin,  \tan\) の符号も分かりますね。

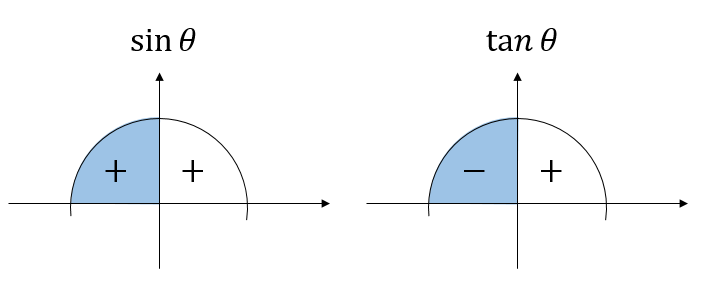
このことを頭に入れておいてから、問題を解き始めます。

\(\cos\)や\(\sin\)の値が分かっているときには、\(\sin^2\theta+\cos^2\theta=1\) に代入します。

$$\begin{eqnarray}\sin^2\theta+\left(-\frac{2}{3}\right)^2&=&1\\[5pt]\sin^2\theta+\frac{4}{9}&=&1\\[5pt]\sin^2\theta&=&1-\frac{4}{9}\\[5pt]\sin^2\theta&=&\frac{5}{9}\\[5pt]\sin\theta>0 より\\[5pt]\sin\theta&=&\frac{\sqrt{5}}{3} \end{eqnarray}$$

\(\sin\) と \(\cos\) の値が揃ったら、\(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\) に代入します。

$$\begin{eqnarray}\tan\theta&=&\frac{\frac{\sqrt{5}}{3}}{-\frac{2}{3}} \\[5pt]&=&\frac{\sqrt{5}}{3}\div\left(-\frac{2}{3}\right)\\[5pt]&=&-\frac{\sqrt{5}}{2}\end{eqnarray}$$

基本問題②場合分け

今回の問題では、\(\sin\)の値が与えられているのですが

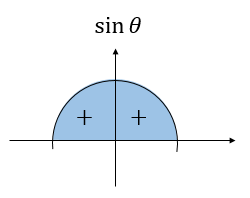
このことから、\(\theta\)が鋭角か鈍角かを判断できません。

よって、\(\cos\)と\(\tan\) の符号も決定することができません。

そのため、答えを出すためには場合分けが必要になります。

最初の手順は先ほどと同じ。

\(\sin\) の値を\(\sin^2\theta+\cos^2\theta=1\) に代入します。

$$\begin{eqnarray}\left(\frac{3}{5}\right)^2+\cos^2\theta+&=&1\\[5pt]\frac{9}{25}+\cos^2\theta&=&1\\[5pt]\cos^2\theta&=&1-\frac{9}{25}\\[5pt]\cos^2\theta&=&\frac{16}{25}\\[5pt]\cos\theta&=&\pm \frac{4}{5} \end{eqnarray}$$

\(\cos\) の符号を決定できないので、このように２つの値が出てきます。

ここから、\(\displaystyle{\cos\theta=\frac{4}{5}}\)のとき、\(\displaystyle{\cos\theta=-\frac{4}{5}}\)のときで場合分けして求めていきます。

\(\displaystyle{\cos\theta=\frac{4}{5}}\)のとき

\(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\) に代入すると

$$\begin{eqnarray}\tan\theta&=&\frac{\frac{3}{5}}{\frac{4}{5}} \\[5pt]&=&\frac{3}{5}\div\frac{4}{5}\\[5pt]&=&\frac{3}{4}\end{eqnarray}$$

\(\displaystyle{\cos\theta=-\frac{4}{5}}\)のとき

\(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\) に代入すると

$$\begin{eqnarray}\tan\theta&=&\frac{\frac{3}{5}}{-\frac{4}{5}} \\[5pt]&=&\frac{3}{5}\div\left(-\frac{4}{5}\right)\\[5pt]&=&-\frac{3}{4}\end{eqnarray}$$

と、このように\(\theta\) が鈍角か鋭角なのか判断できないので２パターンの答えが出てくることになります。

基本問題③\(\tan\)が与えられる

まずは、\(\tan\)の値から\(\theta\)が鋭角、鈍角のどちらになるか考えましょう。

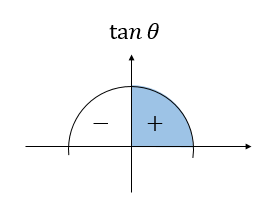
よって、\(\theta\) は鋭角であり\(\cos\) の値は正、\(\sin\) の値も正になることが分かります。

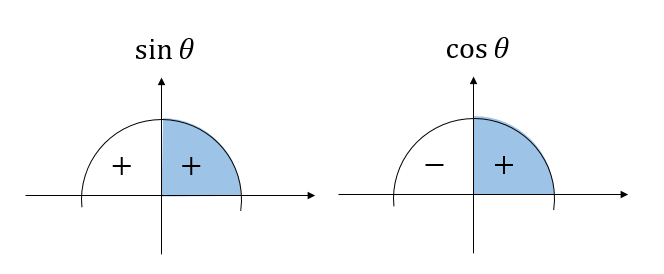
このことを頭に入れておいて計算していきましょう。

\(\tan\) が与えられた場合には、\(\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}\) に代入します。

$$\begin{eqnarray}1+3^2&=&\frac{1}{\cos^2\theta}\\[5pt]10&=&\frac{1}{\cos^2\theta}\\[5pt]\cos^2\theta&=&\frac{1}{10}\\[5pt]\cos\theta>0 より\\\cos\theta&=&\frac{1}{\sqrt{10}}\\[5pt]\cos\theta&=&\frac{\sqrt{10}}{10} \end{eqnarray}$$

\(\cos\) の値が分かったら、\(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\) に代入します。

$$\begin{eqnarray}3&=&\frac{\sin\theta}{\frac{\sqrt{10}}{10}}\\[5pt]3\times \frac{\sqrt{10}}{10}&=&\sin\theta\\[5pt]\sin\theta&=&\frac{3\sqrt{10}}{10} \end{eqnarray}$$

【三角比の相互関係】簡単にせよの問題の解き方は？？

な、なんじゃこりゃ…と、難しそうに感じてしまいますが三角比の相互関係を使えばシンプルな形に変形することができます。

まずは二乗のかっこを展開してやりましょう。

※式が画面から切れる場合には、式を横にスライドしてみてね。

このように計算をしていく過程で、\(\sin^2\theta+\cos^2\theta\) の形を作り、1に変換することで式を簡単にしていくことができます。

【三角比の相互関係】ちょっと応用問題の解き方は？？

今回の問題のように、\(\sin\) と\(\cos\) の和が与えられたときには、両辺を2乗することで答えに近づくことができます。

$$\begin{eqnarray} (\sin\theta+\cos\theta)^2&=&\left(\frac{4}{3}\right)^2\\[5pt]\sin^2\theta+2\sin\theta\cos\theta+\cos^2\theta&=&\frac{16}{9}\\[5pt]1+2\sin\theta\cos\theta&=&\frac{16}{9}\\[5pt]2\sin\theta\cos\theta&=&\frac{7}{9}\\[5pt]\sin\theta\cos\theta&=&\frac{7}{18}\end{eqnarray}$$

このように、両辺を二乗することで\(\sin^2\theta+\cos^2\theta\) の形を作ることができますね！

【三角比の相互関係】まとめ

お疲れ様でした！

三角比の相互関係は、すっごく重要でいろんな場面において活用されます。

数学Ⅱで学習する三角関数においても同様に使っていくことになるので、今のうちに完璧にしておきたいです。

三角比の相互関係を覚えるためには、とにかく問題を解くことが大切です。

公式をにらめっこしているだけでは、やっぱり覚えれません(^^;)

問題を解きながら、手を動かして頭に入れていきましょう！