今回は高校数学Ⅲで学習する
『複素数平面』という単元から
ド・モアブルの定理を使って
2倍角の公式
$$\sin 2\theta=2\sin \theta \cos \theta$$
$$\cos 2\theta=\cos^2 \theta-\sin^2 \theta$$
3倍角の公式
$$\sin 3\theta=3\sin \theta-4\sin^3 \theta$$
$$\cos 3\theta=4\cos^3 \theta-3\cos \theta$$
が成り立つことを証明する方法を解説します。
2倍角の公式の導き方
まずは、ド・モアブルの定理を確認しておきましょう。
ド・モアブルの定理
$$(\cos \theta+i\sin \theta)^n=\cos n\theta+i\sin n\theta$$
2倍角の公式を証明するときには、ド・モアブルの定理のnを2にした式を考えます。
$$(\cos \theta+i\sin \theta)^2=\cos 2\theta+i\sin 2\theta$$
え?なんでn=2で考えるかって?

それはね
2倍角の公式の形を見て
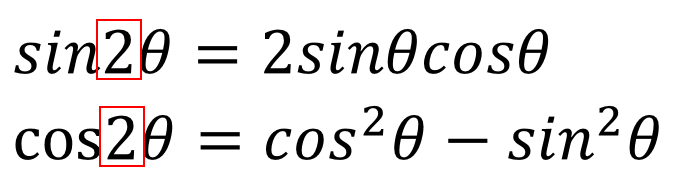
ド・モアブルの定理のn=2の場合を考えれば
2倍角の公式に似た式が作れるんじゃないかなーと予想できるからですね。
そして
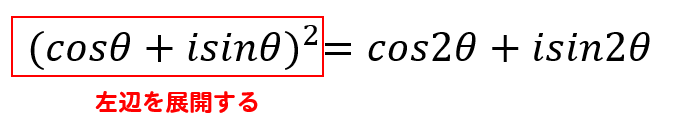
先ほど作った式の
右辺は置いておいて、左辺を展開していきます。
展開は
$$(a+b)^2=a^2+2ab+b^2$$
2乗の展開公式を使ってやっていけばOKです。
すると
\(i^2=-1\)でしたね。この変形を加えてやると
$$=\cos^2 \theta+2i\cos \theta \sin \theta-\sin^2 \theta$$
この式を実部と虚部に分けてやります。

そして、元の式に戻して考えてみると
このようになります。
ここで、左辺と右辺の実部、虚部どうしが等しくなるはずなので

それぞれを等式で表してやると
$$\cos 2\theta=\cos^2 \theta-\sin^2 \theta$$
$$\sin 2\theta=2\sin \theta \cos \theta$$
となり、2倍角の公式を導くことができました。
式の変形をまとめておきます。
$$\cos 2\theta+i\sin 2\theta=(\cos \theta+i\sin \theta)^2$$
$$=\cos^2 \theta+2\cdot \cos \theta\cdot i\sin \theta+i^2\sin^2 \theta$$
$$=\cos^2 \theta+2i\cos \theta \sin \theta-\sin^2 \theta$$
$$=\cos^2 \theta-\sin^2 \theta+(2\sin \theta \cos \theta)i$$
実部と虚部を等式でとってやると
$$\cos 2\theta=\cos^2 \theta-\sin^2 \theta$$
$$\sin 2\theta=2\sin \theta \cos \theta$$
3倍角の公式の導き方
3倍角の公式を導くためには
ド・モアブルの定理をn=3にした式を考えていきます。
$$(\cos \theta+i\sin \theta)^3=\cos 3\theta+i\sin 3\theta$$
これを2倍角のときと同様に左辺を展開していきます。
3乗の展開公式は
$$(a+b)^3=a^3+3a^2b+3ab^2+b^3$$
でしたね。
$$(\cos \theta+i\sin \theta)^3$$
\(i\)の計算は以下を参考にしてください。
$$i^2=-1$$
$$i^3=i^2 \times i=-1\times i =-i$$
この式を実部と虚部にまとめて
元の式に戻してやります。
ここから左辺と右辺の実部、虚部をそれぞれ等式でとってやると

実部から
$$\cos 3\theta=\cos^3\theta-3\cos\theta\sin^2\theta$$
$$=\cos^3\theta-3\cos\theta (1-\cos^2 \theta)$$
$$=\cos^3\theta-3\cos\theta+3\cos^3\theta$$
$$=4\cos^3\theta-3\cos\theta$$
よって
$$\cos 3\theta=4\cos^3\theta-3\cos\theta$$
を導くことができました。
虚部からは
$$\sin 3\theta=3\cos^2\theta\sin\theta-\sin^3\theta$$
$$=3(1-\sin^2\theta)\sin\theta-\sin^3\theta$$
$$=3\sin\theta-3\sin^3\theta-\sin^3\theta$$
$$=3\sin\theta-4\sin^3\theta$$
よって
$$\sin 3\theta=3\sin\theta-4\sin^3\theta$$
を導くことができました。
式変形には、以下の性質を利用しています。
\(\sin^2\theta+\cos^2\theta=1\)より
$$\sin^2\theta=1-\cos^2\theta$$
$$\cos^2\theta=1-\sin^2\theta$$
ド・モアブルの定理から2倍角・3倍角のまとめ
導き方の手順はとってもシンプルです。
2倍角を導きたいときには\(n=2\)で考えて
左辺と右辺の実部、虚部を見比べる。
3倍角を求めたいときには\(n=3\)で考えて
左辺と右辺の実部、虚部を見比べる。
それだけです。
途中の計算部分は少し複雑なので
見て、理解した!
ではなくて
手を動かして、理解した!
という状態にしておいてくださいね
ファイトだー!












コメントを残す