こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する指数関数の単元から「グラフの位置関係」についてイチから解説します。
取り上げる問題はこちら!
次の指数関数のグラフは、\(y=2^x\)のグラフとどのような位置関係にあるか答えなさい。
(1)\(y=16\cdot 2^x\)
(2)\(y=\frac{1}{8}\cdot 2^x +1\)
(3)\(y=\left(\frac{1}{2}\right)^x-2\)
「どこを見ればいいの?」「どうやって式変形するの?」
ということで疑問を感じやすい問題だと思うので、イチからていねいに解説していきますね!
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(1)解説
まずはベースとなっている \(y=2^x\) に近づくように式変形をしましょう!

そしたら、ベースとなる \(y=2^x\) に対して、どの部分が変化しているのかに注目します。
すると、今回は次のように変化していることがわかりますね。
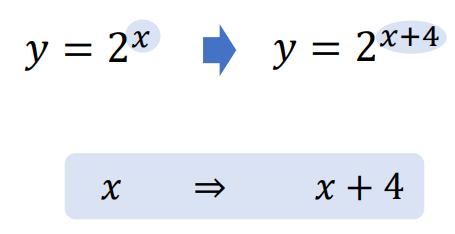
つまり、この部分から
\(x\)軸方向に\(-4\)だけ平行移動している
ということが読み取れます。
グラフをかくとこんな感じですね!
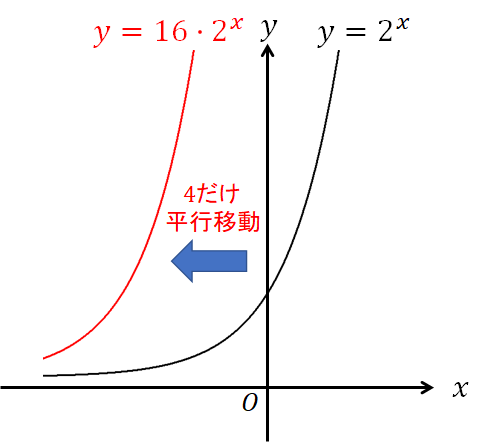
(2)解説
(1)と同じように、\(y=2^x\)に近づくように式変形します。
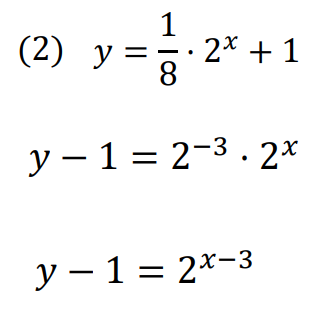
\(+1\)は左辺にもってきておくと、式の変化が読み取りやすくなります。
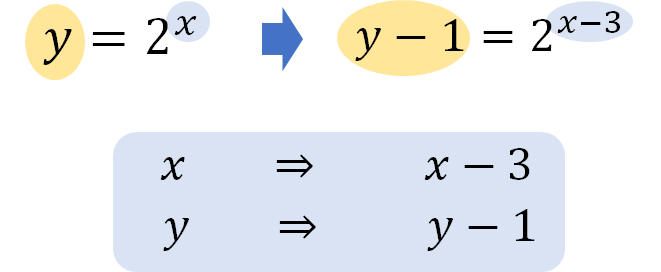
今回は \(x,y\) がそれぞれ上のように変化していることがわかりますね。
つまり、この部分から
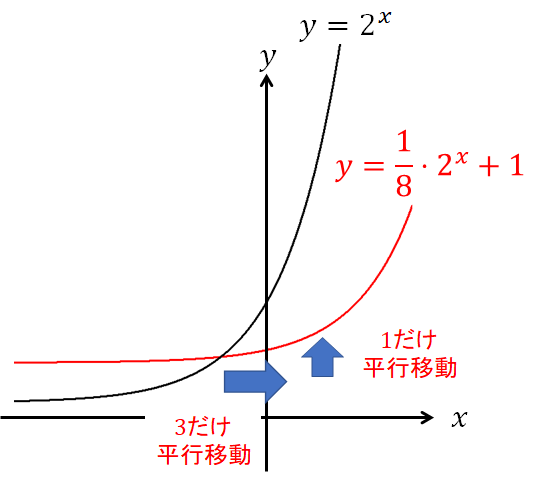
\(x\)軸方向に\(3\)、\(y\)軸方向に\(1\)だけ平行移動している
ということが読み取れます。
グラフにするとこんな感じですね!
(3)解説
では、これまでと同じように式を変形していきましょう!
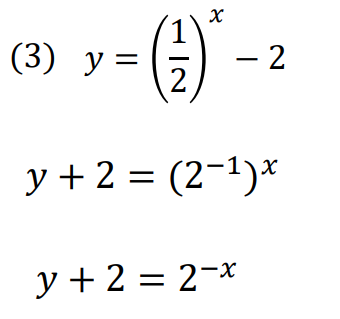
そして、どの部分が変化しているか読み取りましょう。

すると、\(x\)の部分は符号がチェンジされていますね。
これは「対称移動」を表しています。
【対称移動のポイント】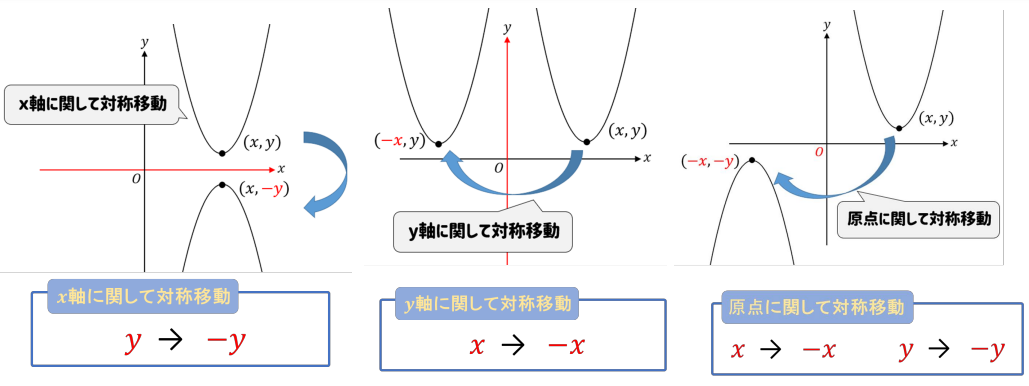
上の図を見ると、\(x\)の符号がチェンジするのは「\(y\)軸に関して対称移動」した場合です。
よって、
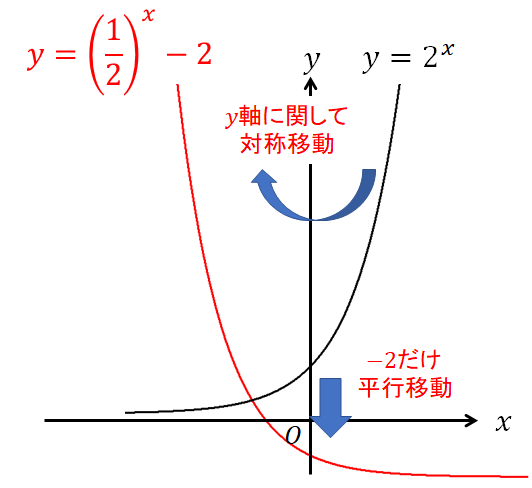
\(y\)軸に関して対称移動し、\(y\)軸方向に\(-2\)だけ平行移動している
ということが読み取れます。
グラフにするとこんな感じです!
まとめ
お疲れ様でした!
というわけで、位置関係の読み取り方について理解してもらえましたか??
「式変形する」⇒「変化している部分を読み取る」⇒「平行移動?対称移動?を考える」
この3STEPで見ていけばいいですね^^
慣れたらサクサク解ける問題だと思うので、たくさん練習してテストで完答できるようにがんばってください(‘ω’)ノ
では、以上!













コメントを残す