こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する指数関数の単元から「対数不等式の解き方」についてイチから解説します。
レベル別の練習問題を使って徐々にレベルアップしていきましょう!
今回取り上げる問題はこちら。
【練習問題】
(初級)
(1)\(\log_3{x}>2\)
(2)\(\log_{0.5}≧2\)
(中級)
(3)\(\log_2{(x+1)}+\log_2(x-2)<2\)
(4)\(2\log_{0.5}(3-x)≧\log_{0.5}4x\)
(上級)
(5)\(\log_3{(x-2)}≧\log_9{(x+10)}\)
(6)\((\log_{0.5}x)^2-\log_{0.5}{x^2}-8>0\)
これらが全部クリアできたら対数不等式はバッチリです!
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
対数不等式の解き方
まずは対数不等式を解く流れを確認しておきましょう。
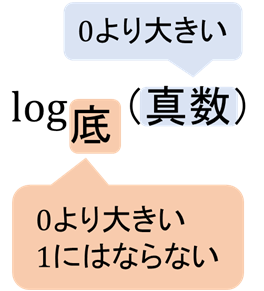
STEP1 底、真数条件をチェック!
まずは底、真数の条件をチェックして\(x\)の範囲を出しておきます。
STEP2 左辺、右辺をlogの形にそろえて真数を比較する
次に左辺、右辺をlogの形にそろえて真数どうしを比較します。
ここで注意するのは「底の大きさ」です。
底が1より大きい場合は、不等号の向きをそのまま
底が1より小さい場合は、不等号の向きを逆にして取り出します。

STEP3 不等式を解く
STEP2で取り出した不等式を解きます。
ここで求めた\(x\)の範囲とSTEP1で求めた範囲の共通部分を見つけたらゴールです。
では、この流れに沿ってそれぞれの問題を解説していきますね!
(1)(2)の解説
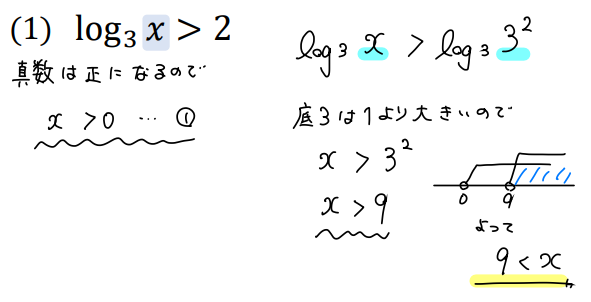
まずは真数条件から、\(x>0 \cdots①\) という範囲を求めています。
そこからlogの形にそろえるため、右辺を「\(2=\log_3{3^2}\)」と変形。
底3が1より大きいので、不等号の向きはそのままで真数を取り出しています。
不等式を解くと、\(x>9\)と出てきたので、数直線をかいて①との共通部分を取り出してゴールです!
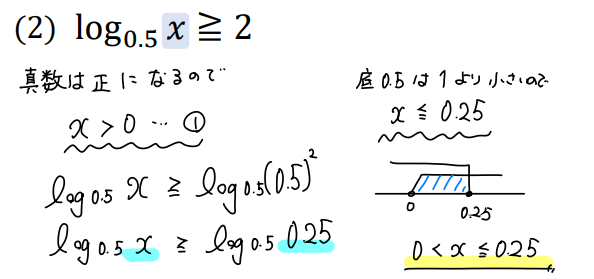
(1)と流れは同じですが、底が1より小さくなっているので真数を比較するときには不等号を逆にするのをお忘れなく!
(3)対数をまとめる

さぁ、この問題はやることが盛りだくさんですね(^^;)
まずは真数条件を求めておきましょう。
真数が2か所ありますので、それぞれの値がともに正となるように範囲を求めます。
そこからlogを1つにまとめていきましょう。
使ってるのは、\(\log_2{A}+\log_2{B}=\log_2{AB}\) という性質ですね。たし算は積でまとめます!
そして、右辺もlogの形に統一して真数どうしを比較。(底が1より大きいので不等号はそのまま)
あとは不等式を解いていき、①の範囲と共通する部分を抜き出したらゴールです!
(4)係数に注意!

基本的な流れは(3)と同じなのですが、
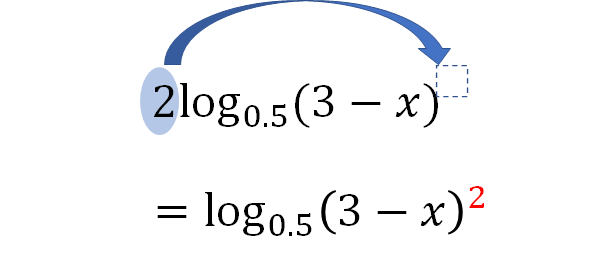
この部分に注意ですね!
係数がついていると真数どうしの比較ができないので変形しておきましょう。
底が1よりも小さくなっているので、真数を比較するときに不等号を逆にするのをお忘れなく!
(5)底をそろえる

底がそろっていないので、底の変換が必要になります。
底を変換したときには分数の形になってしまうので、分母を払って式をシンプルに変換してくださいね!
底が揃ったら、あとの流れはいつも通りって感じですね^^
(6)置き換えを利用

※計算が大変そうだったので、途中から底0.5を\(\frac{1}{2}\)に変換して計算しています。
ここでは置き換えを利用して計算しています。
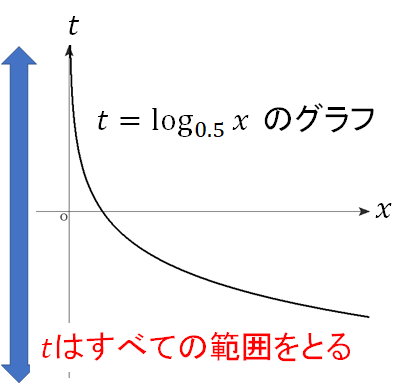
置き換えを利用した場合、置き換えた文字の範囲を求めるのが常ですが、グラフをかいてイメージできる通り、\(t\)はすべての範囲となるため特に気にしなくてOKです。
そして、次のように不等式を置き換えています。
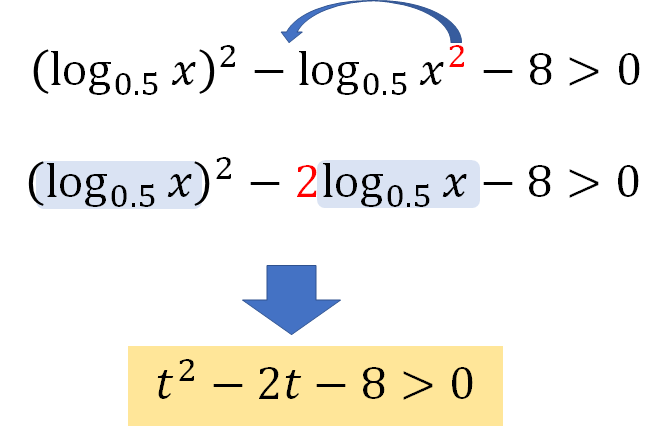
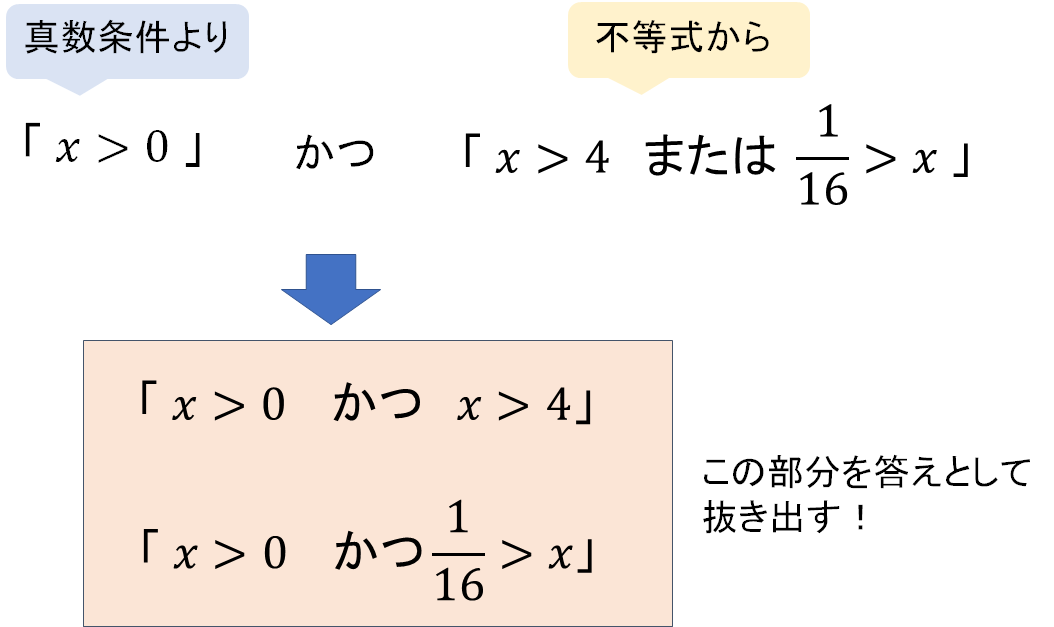
あとは「不等式を解く」 ⇒ 「\(t\)をもとに戻して\(x\)の範囲を求める」といった流れで進めてください。
最後の範囲取りがちょっとややこしいですが、次のように考えてください。
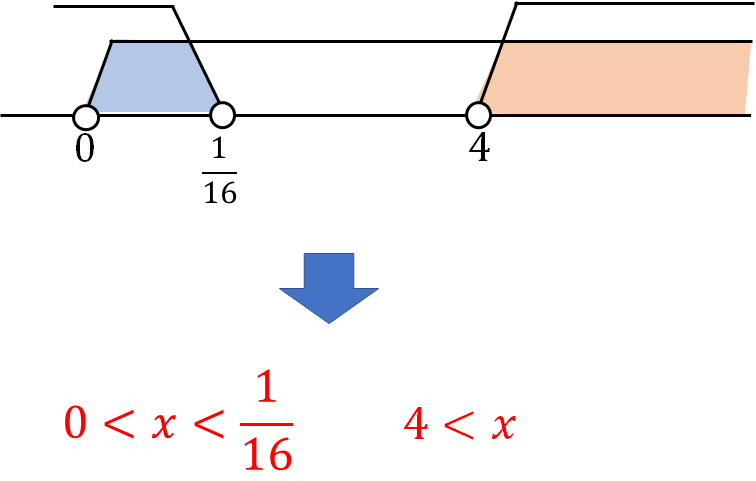
まとめ
お疲れ様でした!
これで対数不等式はバッチリかな??
計算過程が多くて大変だけど、入試にも出てきやすい問題だからしっかりと習得しておきたいね^^
「真数条件のチェック忘れ」「底が1より小さい場合の不等号ミス」
こういったところで失点しちゃう人が多いから注意しておいてね!
では、以上!















コメントを残す