こんにちは!数スタの小田です。
今回は中3のラストに学習する「標本調査」について、よく出る問題をパターン別に解説していきます。
動画講義を使えばサクッと習得できるので、こちらも活用してくださいね^^
標本調査、全数調査のどっち?
【問題】次の調査は、全数調査と標本調査のどちらが適切か。
(1)かんづめの品質検査
(2)あるクラスの出欠
(3)ある湖の水質検査
(4)あるクラスの進路調査
まずは全数、標本調査の違いについて確認しておきましょう。

全部調べる必要がある ⇒ 全数調査
全部調べるのはムリ ⇒ 標本調査
このように判断していきます。
というわけで、問題にある調査がどちらにあたるのか考えてみましょう。

すると、こんな感じで調査方法を判断することができますね!
標本の選び方として適切なのは?
【問題】次の標本調査について、標本の選び方として正しいものを選びなさい。
ある中学校の全生徒400人について、睡眠時間を調査する。
(1)中学1年生の中から選ぶ。
(2)知り合いに声をかけて選ぶ。
(3)全校生徒の中からくじ引きで選ぶ。
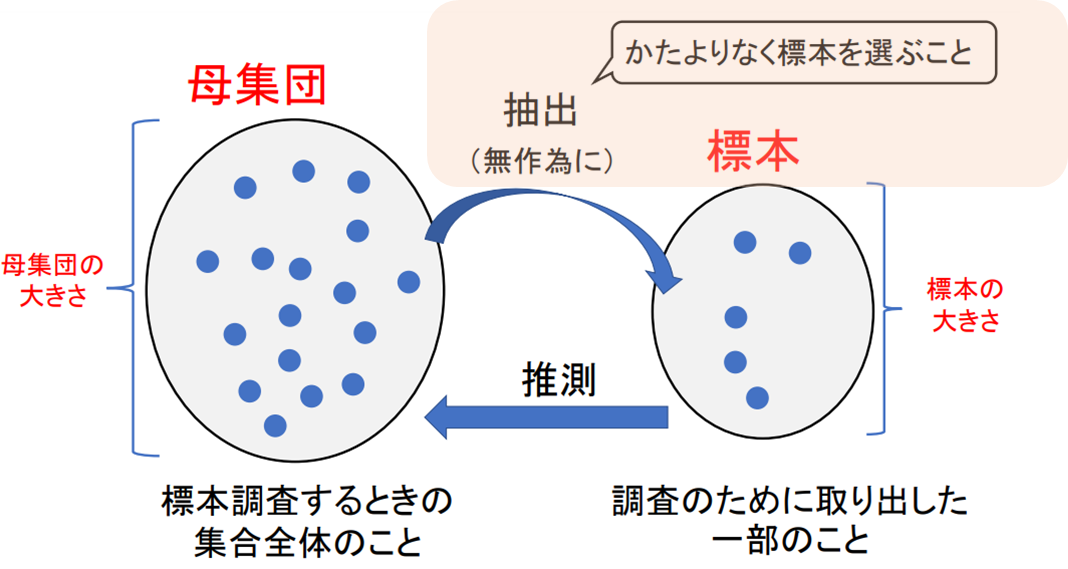
標本は必ず無作為(ランダム)にかたよりなく選ばれる必要があります。
そのため、かたよりがあるような選び方を排除していきましょう。

よって、(3)が標本の選び方として正しいことがわかります。

標本調査の利用問題
問題①
袋の中に入っている青い玉の個数を\(x\)個とすると
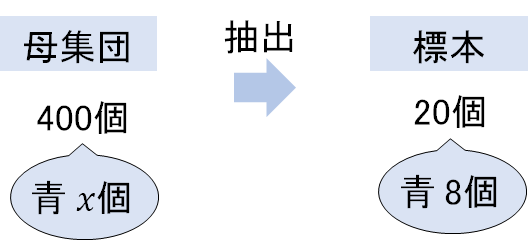
このような状態になっていますね。
標本の中に含まれる青の割合は、
$$\frac{8}{20}=\frac{2}{5}$$
となるので、母集団に含まれる青も同様に\(\frac{2}{5}\)の割合だろうと推測できます。
よって、
$$400\times \frac{2}{5}=160$$
答え
およそ160個
もしくは、全体、青の個数を比例式にして次のように解いてもOKです。
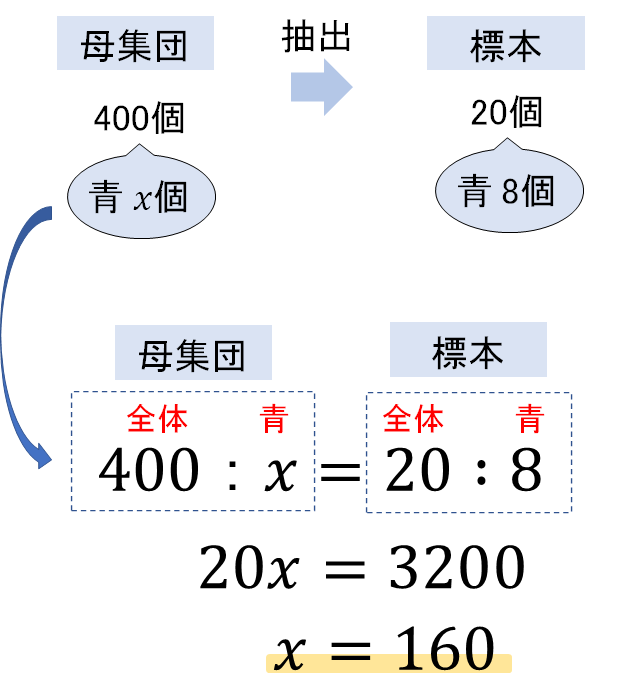
自分のしっくりくる方がやってください^^
問題②
池にいる魚の総数を\(x\)匹とすると
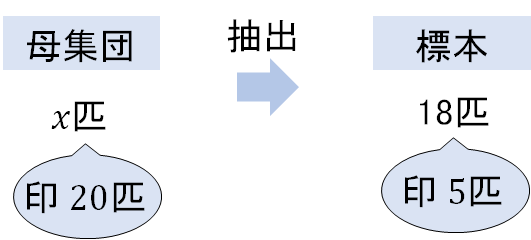
このような状態になっていますね。
標本に含まれる印のついた魚の割合は、\(\frac{5}{18}\) なので
母集団に含まれる印のついた魚の割合も同様に\(\frac{5}{18}\)になると推測できます。
よって、
$$\begin{eqnarray}x\times \frac{5}{18} &=&20\\[5pt]5x&=&360\\[5pt]x&=&72\end{eqnarray}$$
答え
およそ72匹
比例式を使った次のように解いてもOKです!
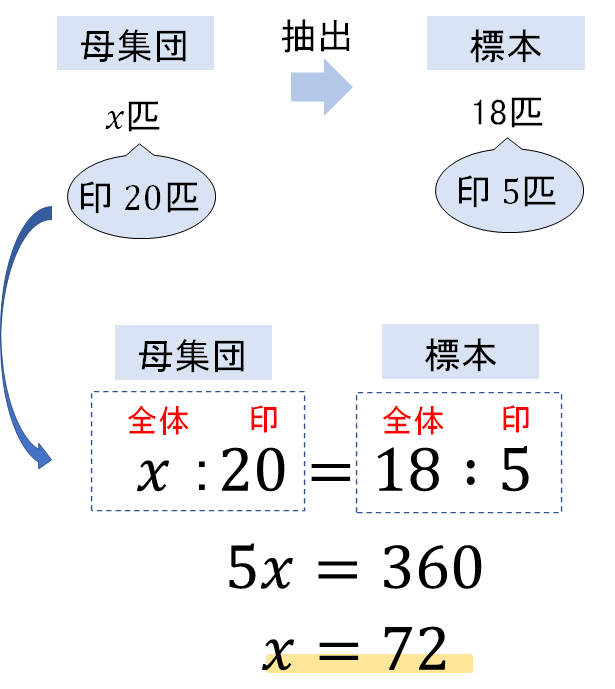
比例式を使った方が発想がシンプルでかんたんかもしれませんね^^
問題③
はじめの箱の中に入っていた白玉の個数を\(x\)個とすると
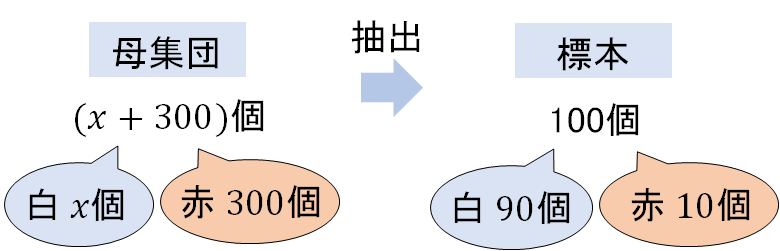
こんな状態になっています。
今回は母集団の全体が\((x+30)\)個となってしまい、ちょっとややこしいので全体の数ではなく、白と赤の内訳の割合に注目して式を作っていきましょう。
ここでは比例式を使うとスムーズです。
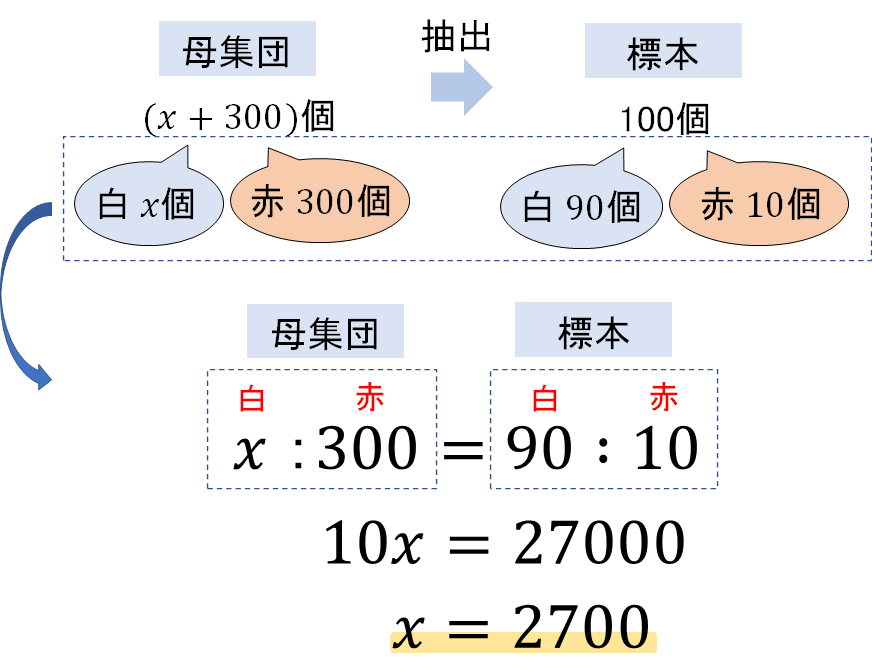
答え
およそ2700個
まとめ
お疲れ様でした!
これで標本調査はバッチリかな?
入試に出やすいのは最後の方で練習してもらった利用問題です。
母集団、標本の情報を整理して割合、比例式がつくれるように練習しておいてくださいね!
というわけで、以上!









コメントを残す