こんにちは！数スタの小田です。
今回は高校数学Ⅱで学習する対数関数の単元から「最高位の数字の求め方」についてイチから解説します。
取り上げる問題はこちら！
今回の内容をサクッと理解したい方は、こちらの動画がおススメです！
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾
Contents
【例題】最高位を求める手順
では、こちらの例題を使って最高位を求める手順を紹介します。
STEP1 logの値を求めよう！
STEP2 10の累乗の形にして分割する！
STEP3 小数部分の値の範囲をチェックする！
※かんたんな問題では与えられた小数をそのまま使えばはさみ込むことができます。ですが、応用になると与えられた対数の値をもとにして\(\log_{10}{5}, \log_{10}{6} \)といった値を求めさせられる場合もあります。
不等式を作れたら、両端の値をシンプルになるよう変換していきましょう。
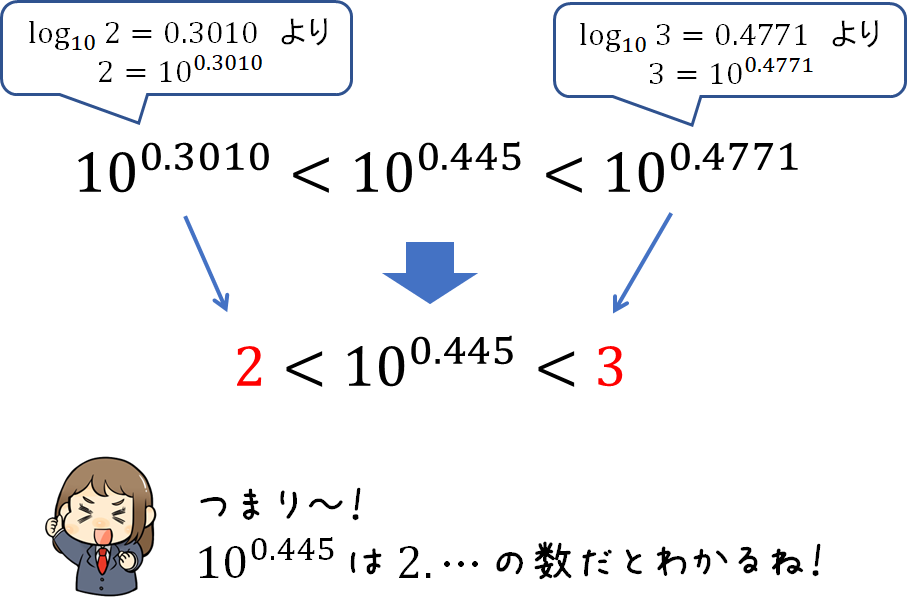
STEP4 最高位が求まる！
ここまれの流れを振り返るとこんな感じになります。
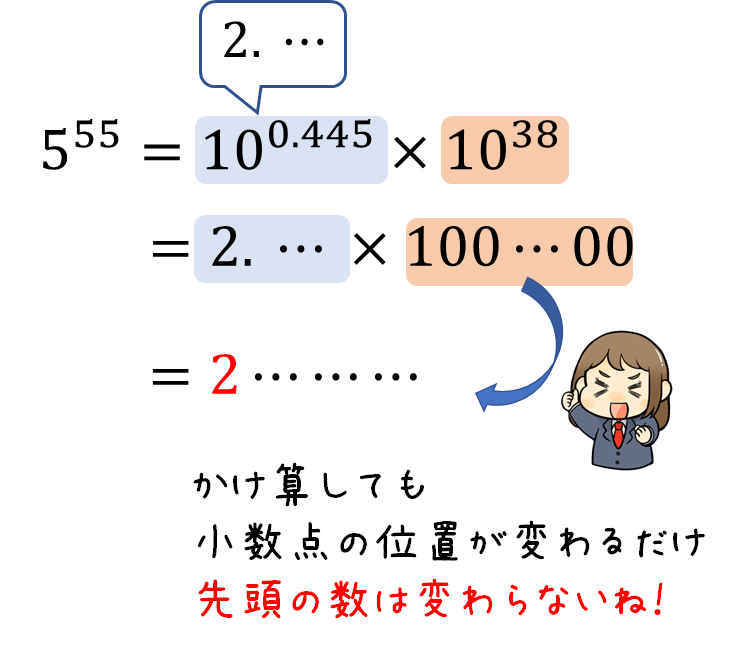
というわけで、\(5^{55}\)の最高位の数は2だとわかりました。
答え
$$2$$
どうですか、求め方の流れは理解してもらえましたか？？
次の練習問題を使って理解を深めておきましょう！
練習問題にチャレンジ！
解答＆解説
まとめ
お疲れ様でした！
これで最高位の数はバッチリかな？
最後に解法の流れをまとめた画像を貼っておくので、忘れたときの振り返り用として活用してください＾＾
では、今回は以上！
コメントを残す