【指数関数】グラフのかき方をイチから！マイナスがついてるときは？

こんにちは！数スタの小田です。

今回は高校数学Ⅱで学習する指数関数の単元から「グラフのかき方」についてイチから解説します。

取り上げる問題はこちらの3題！

 

今回の内容をサクッと理解したい方は、こちらの動画がおススメです！

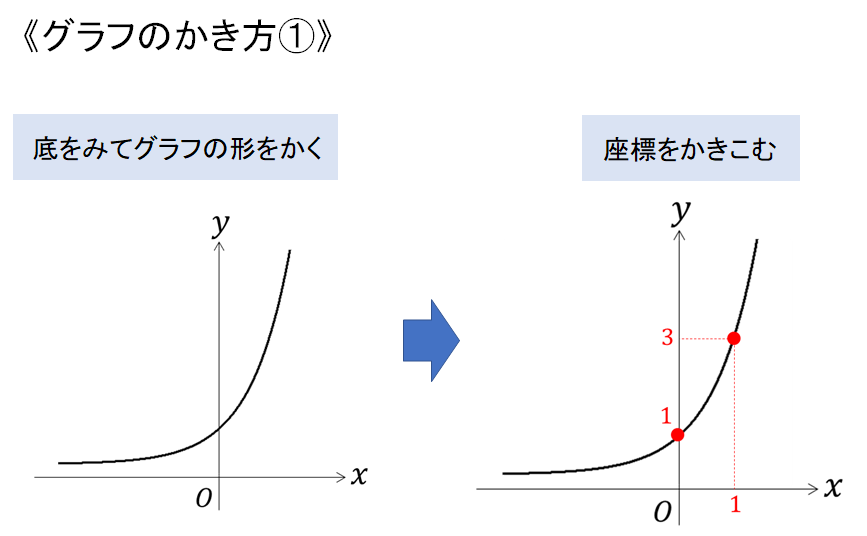
指数関数のグラフの形

指数関数のグラフは次の2パターンの形になります。

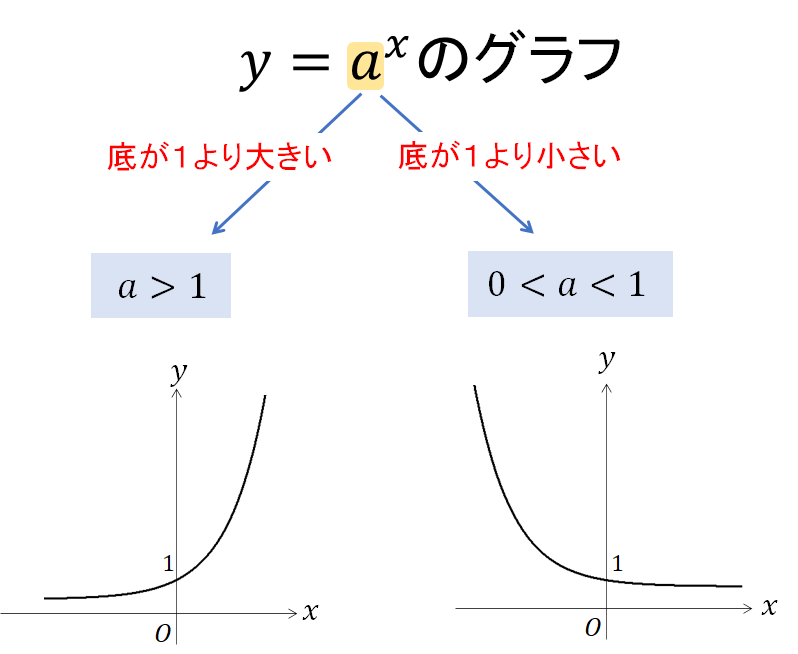
底の大きさに注目して、1より大きかったらグイーンと上がっていくようなグラフ。

底が1より小さかったらグイーンと下がっていくグラフになります。

 

 

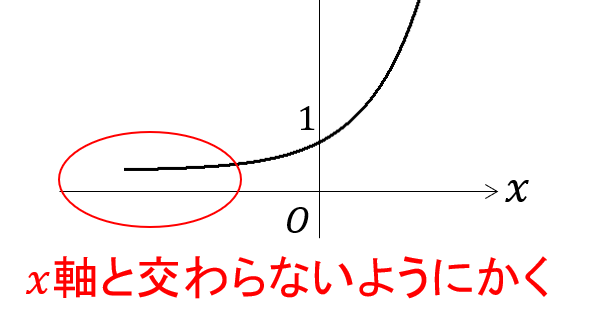
このように\(x\)軸とは絶対に交わらないようにかいてくださいね！

 

では、冒頭で取り上げた3つの関数について、グラフのかき方を見ていきましょう！

（1）底が１より大きいグラフ

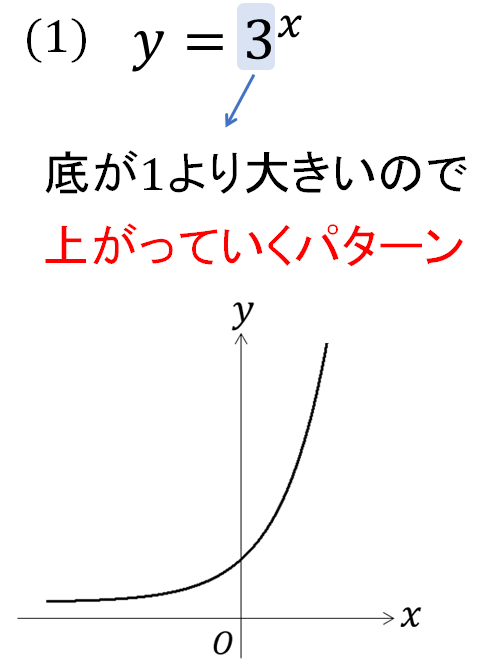
まずは底の大きさに注目して、グラフの形を判断しましょう！

今回は底が「3」で1より大きくなっていることから、上のようにグイーンと上がっていくようなグラフをかきます。

 

グラフの形がつくれたら、次に座標をとっていきます。（座標は2点とれたらOK）

座標はどこでもいいのですが、シンプルでわかりやすい\(x=0,1\)の2点をとるのが一般的！

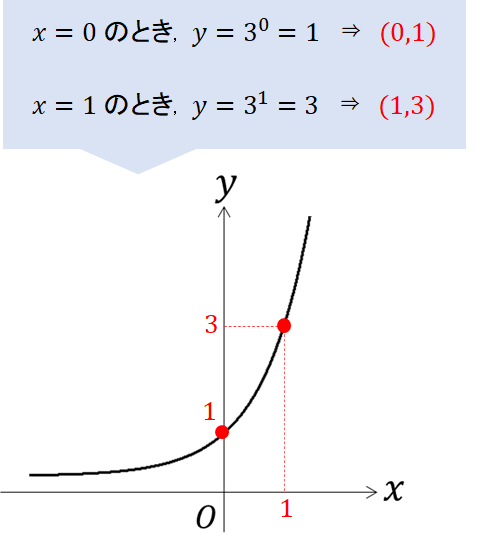
こんな感じでグラフに座標を書き込めれば完成です！

 

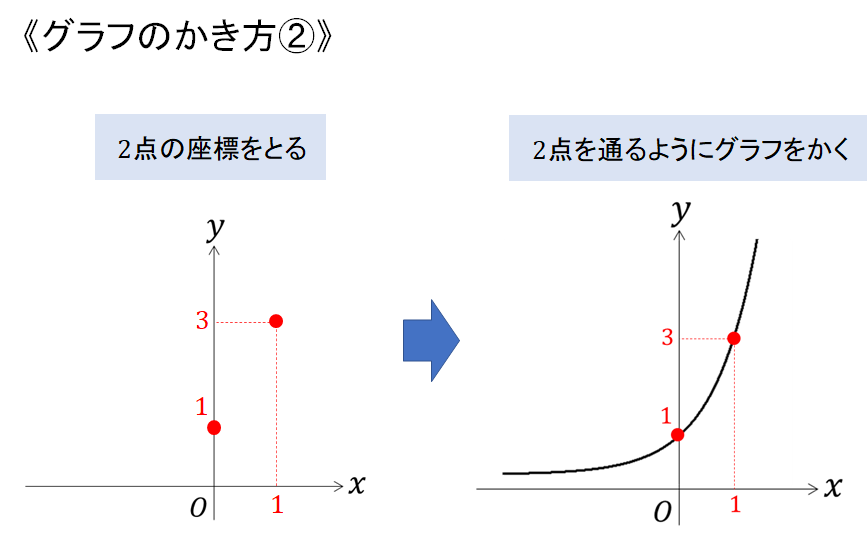
今回は「グラフの形　⇒　座標」の順で書いてみましたが

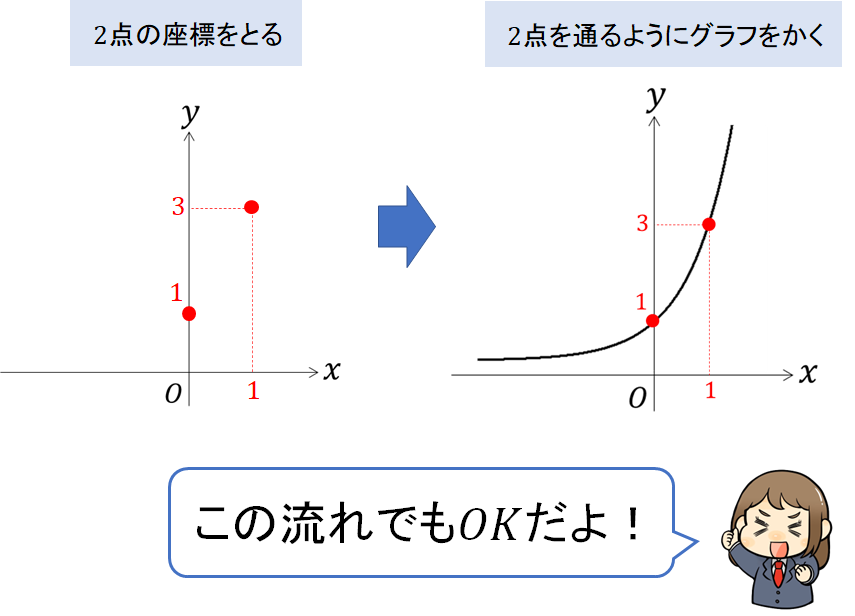
このように「座標　⇒　グラフの形」という順でもOKです＾＾

座標をとってからグラフを書いた方がより正確な形のグラフがかけるかな！

（2）底が１より小さいのグラフ

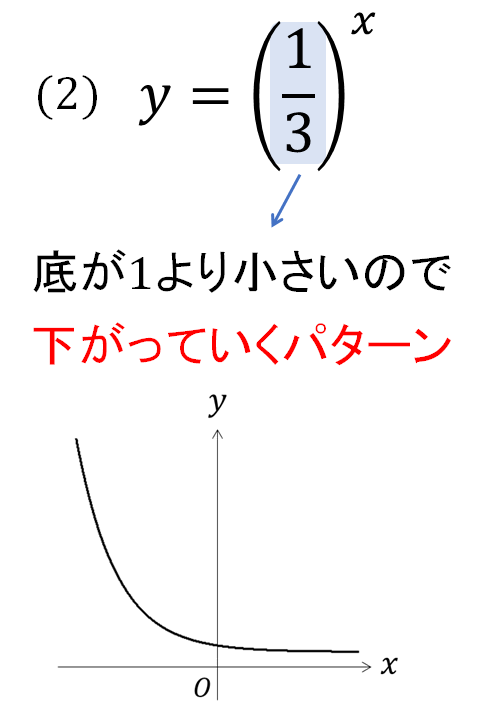
今回の底は「\(\frac{1}{3}\)」で1より小さいので、グイーンと下がっていくグラフになりますね。

グラフの形が書けたら座標をとっていきましょう。

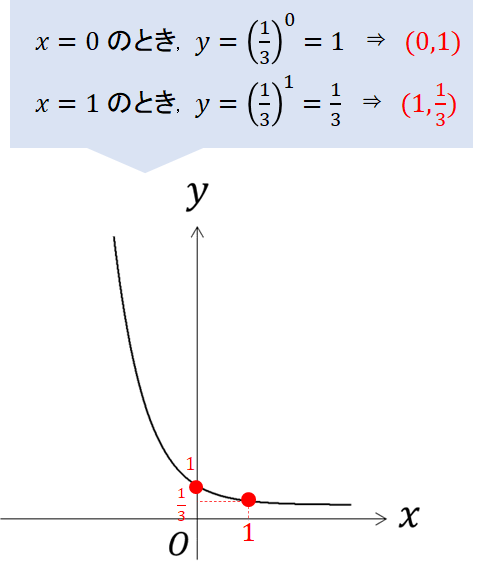
これで完成！

なのですが…\(\left(1, \frac{1}{3} \right)\)の点が書き込みずらい！！

と感じた方は、無理して\(x=1\)の座標をとらなくてもOK。

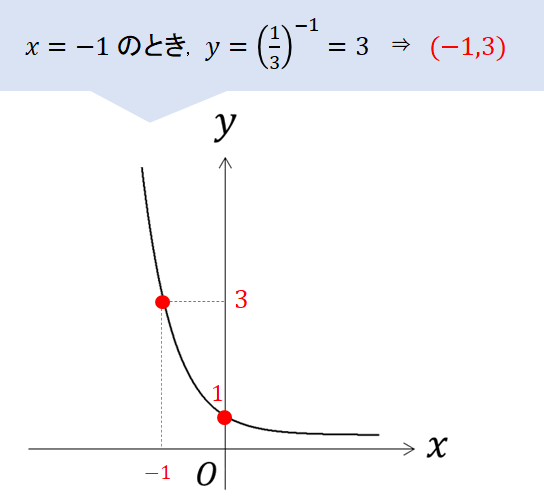
このように空いたスペースに書き込めるような座標を見つけてやればいいですよ＾＾

（とにかく2点の座標が書き込まれていればOK）

（3）マイナスがついているグラフ

このように勘違いしがちですが、底が0以下になることはありません！

 

この関数は次のように見ていきましょう。

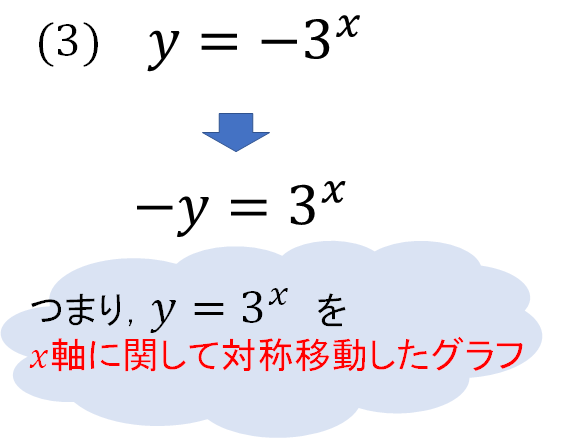
なので、まずは\(y=3^x\)のグラフをイメージして、それを\(x\)軸でパタンと折り返したグラフをかきます。

 

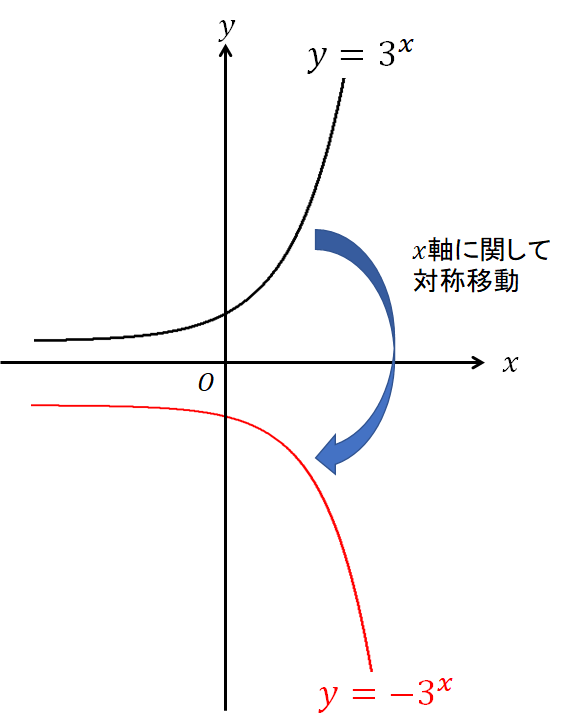
次に座標をとっていけばグラフの完成です！

 

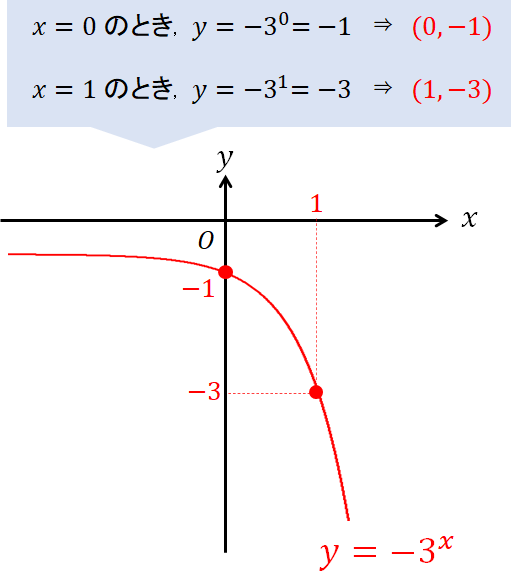
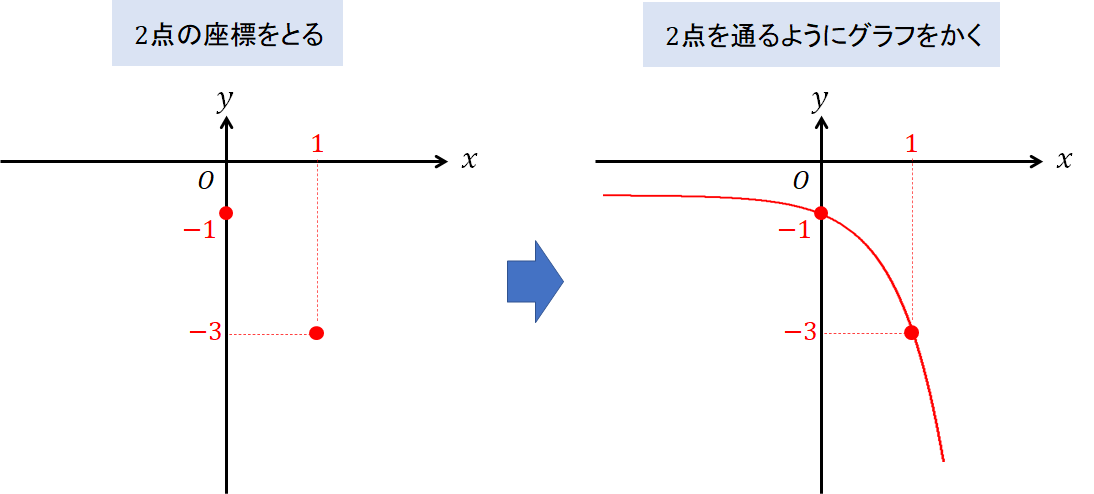
「でも、対称移動を考えるとかちょっとメンドイです…」

と感じたあなたは「座標 ⇒ グラフの形」の順でやるとラクにかけますよ＾＾

まとめ

お疲れ様でした！

これで指数関数のグラフはバッチリかな？

やり方がわかったら、たくさん練習してスラスラかけるようにしておきましょうね(‘ω’)ノ

では、以上！