3乗根の分数の有理化はどうやる？考え方をイチから解説！

こんにちは！数スタの小田です。

今回は高校数学Ⅱで学習する指数関数の単元から「3乗根の有理化」についてイチから解説します。

取り上げる問題はこちら！

 

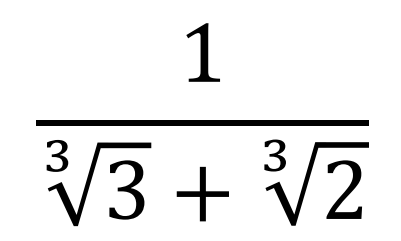
今回の内容をサクッと理解したい方は、こちらの動画がおススメです！

3乗根の有理化の考え方！

有理化って、符号をチェンジしたものをかければいいんでしょ？楽勝、楽勝～♪

と、これまでの有理化のやり方でやろうとすると…

 

これまで扱ってきたルート（平方根）は2乗をすると、ルートをなくすことができましたね。

なので、

この乗法公式を利用することで、分母を2乗の形にしてルートをなくしていました。

こんな感じ！

 

一方で、3乗根のルートをなくすためには3乗の形をつくる必要があります！

 

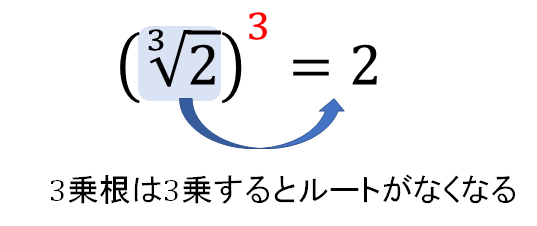
というわけで、分母に3乗の形をつくるために

この乗法公式を活用していきます。

 

この乗法公式を参考にして、次のパーツを分母、分子にかけることになります。

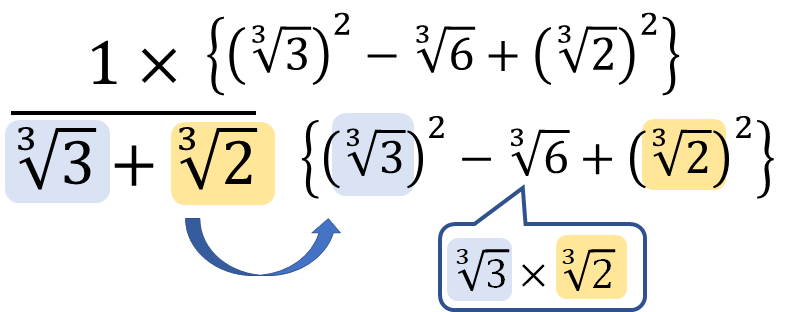
ちょっとわかりづらいですが、分母を2つの項を見る。

そこから「2乗、かけて符号チェンジ、2乗」というパーツをつくる感じです！

 

あとは計算あるのみ！

 

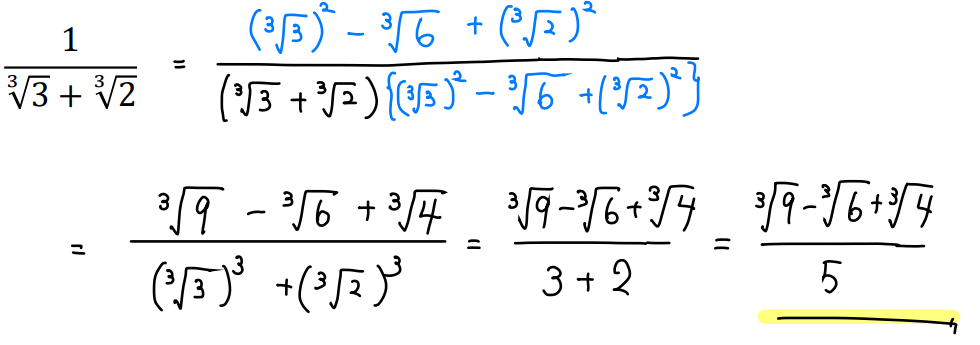
というわけで、3乗根の有理化はちょっと複雑ですが、

この乗法公式を覚えておけば、その場でパーツを見つけることができますね＾＾

 

一応、3乗根の有理化テンプレートを作っておくので参考にしてください。

練習問題にチャレンジ！

それでは、理解度をチェックするために練習問題にチャレンジしてみましょう。

 

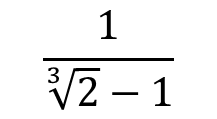
まとめ

お疲れ様でした＾＾

これで3乗根の有理化はバッチリかな？

途中式がややこしくなっちゃうので、暗算でやろうとせずにていねいに式をかきながらやっていきましょうね！

 

では、以上！